Jokainen koululainen tietää, että aina hypotenuusin neliö on yhtä suuri kuin katetiden summa, joista jokainen on koholla neliöön. Tätä lausuntoa kutsutaan pythagores teoreiksi. Se on yksi Trigonometrian ja matematiikan tunnetuimmista teoreemioista. Harkitse sitä tarkemmin.

Suorakaiteen muotoinen kolmio

Ennen siirtymistä Pythagoreo-lauseeseen, jossa hypotenuusin neliö on yhtä suuri kuin kateton summa, joka kohoaa neliöön, pitäisi harkita suorakaiteen muotoisen kolmion käsite ja ominaisuudet, joista teorema on kelvollinen.

Triangle on tasainen luku, jossa on kolme kulmaa ja kolme puolta. Suorakulmainen kolmio, joka seuraa sen nimestä, on yksi suorakulma, eli tämä kulma on 90 o.

Kaikkien kolmioiden yleisistä ominaisuuksista tiedetään, että kaikkien kolmen kulman summa on 180 O, ja tämä tarkoittaa, että suorakulmaiselle kolmion, kahden kulman summa, joka ei ole suora, on 180 O - 90 O \u003d 90 o. Viimeisin seikka tarkoittaa, että mikä tahansa kulma suorakulmaisessa kolmiossa, joka ei ole suora, on aina alle 90 o.

Suorasta kulmasta vastaava puoli on tavanomaista kutsua hypotenuusiksi. Muut muut osapuolet ovat kolmion asiakkaita, ne voivat olla yhtä suuria ja voivat poiketa toisistaan. Trigonometriasta tunnetaan, että suurempi kulma, johon sivu on kolmiossa, sitä suurempi tämän sivun pituus on. Tämä tarkoittaa sitä, että suorakulmaisessa kolmikulmiossa hypotenuusin (90 o: n kulmaa vasten) on aina enemmän kuin mikään kateto< 90 o).

Matemaattinen nauhoitus Theorem Pythagora

Tämä teorema toteaa, että hypotenuusin neliö on yhtä suuri kuin katetiden määrä, joista kukin on aiemmin kohotettu neliöön. Matemaattisesti polttaa tämä sanamuoto, harkitse suorakulmaista kolmiota, jossa osapuolet A, B ja C ovat vastaavasti kaksi luokkaa ja hypotenoja. Tässä tapauksessa teorema, joka on formuloitu hypotenuusin neliöksi, on yhtä suuri kuin katetesi neliöiden summa, voidaan esittää seuraavaa kaavaa: C2 \u003d A 2 + B2. Täältä voidaan saada muita tärkeitä kaavojen käytännön kannalta: A \u003d √ (C2 - B2), B \u003d √ (C2 - A 2) ja C \u003d √ (A 2 + B 2).

Huomaa, että suorakulmainen tasapuolinen kolmio, eli A \u003d B, sanamuoto: hypotenuusin neliö on yhtä suuri kuin katetesi summa, joista kukin korotetaan neliöön, matemaattisesti tallennetaan: C2 \u003d A 2 + B 2 \u003d 2A2, jossa tasa-arvo virtaa: C \u003d A√2.

Historiallinen viite

Pythagoran teorea, joka tähtää, että hypotenuusin neliö on yhtä suuri kuin katetiden määrä, joista kukin korotettiin neliöön, tunnettiin kauan ennen kuin kuuluisa kreikkalainen filosofi kiinnitti huomiota siihen. Monet antiikin Egyptin papyrus sekä savi merkkejä Babylonialaiset vahvistavat, että nämä kansakunnat käyttivät suorakulmaisen kolmion sivujen merkittyä ominaisuutta. Esimerkiksi yksi ensimmäisistä Egyptin pyramidista, Hefrenin pyramidi, jonka rakentaminen kuuluu XXVI-luvulle BC (2000 vuotta ennen Pythagoran elämää), rakennettiin kuvasuhteen perusteella 3x4x5 suorakulmion kolmio.

Miksi sitten tällä hetkellä teorema on kreikan nimi? Vastaus on yksinkertainen: Pythagoras on ensimmäinen, joka matemaattisesti osoittanut tämän teoreen. Säilytetyssä Babylonian ja Egyptin kirjallisissa lähteissä vain sen käyttöä viitataan, mutta matemaattisia todisteita ei anneta.

Uskotaan, että Pythagoras osoittautui teoreen käsiteltäväksi käyttämällä samankaltaisten kolmioiden ominaisuuksia, jotka hän sai, kun hän sai korkeuden suorakaiteen muotoisessa kolmiossa 90 O: n kulmasta hypotenuusiin.

Esimerkki Pythagores-teoreen käytöstä

Harkitse yksinkertaista tehtävää: on tarpeen määrittää kaltevan portaikon L pituus, jos tiedetään, että sillä on korkeus H \u003d 3 metriä ja etäisyys seinästä, johon portaikko on, kunnes sen jalka on p \u003d 2,5 metriä.

Tässä tapauksessa H ja P ovat katekotteja, ja l on hypotenuse. Koska hypotenuuspituus on yhtä suuri kuin katetesi neliöiden summa, saamme: L 2 \u003d H2 + P2, mistä L \u003d √ (H2 + P2) \u003d √ (3 2 + 2,5 2) \u003d 3,905 metriä tai 3 m ja 90, 5 cm.

Pythagoraan lause: Kartsiin perustuvien neliöiden neliöiden summa ( a. ja b.), on yhtä suuri kuin hypotenuussa rakennetun neliön neliö ( c.).

Geometrinen sanamuoto:

Aluksi teorema formuloitiin seuraavasti:

Algebrallinen sanamuoto:

Eli merkitsee kolmion hypotenuusin pituutta c. ja katetiden pituus a. ja b. :

a. 2 + b. 2 = c. 2

Molemmat sanamuodat ovat vastaavia, mutta toinen sanamuoto on alkeisempaa, se ei vaadi alueen käsitettä. Toisin sanoen toinen lausunto voidaan tarkistaa, mikään ei tiedä alueesta ja mittaa vain suorakulmion kolmiojen pituus.

Pythagoran Reverse Theorem:

Todiste jstk

Tällä hetkellä 367 näyttöä tästä teoremista kirjattiin tieteelliseen kirjallisuuteen. Todennäköisesti Pythagora Theorem on ainoa teorea, jolla on niin vaikuttava määrä todisteita. Tällainen lajike voidaan selittää vain geometrian teorian perustavanlaatuisella arvolla.

Tietenkin se on käsitteellisesti niitä voidaan jakaa pieneen määrään luokkia. Tunnetuin niistä ovat: Todisteet avaruusmenetelmällä, aksiomaattisella ja eksoottisella todisteilla (esimerkiksi differentiaaliyhtälöillä).

Tällaisten kolmioiden kautta

Seuraava todistus algebraalisesta sanamuodosta on yksinkertaisin näyttöön käynnissä suoraan aksiomista. Erityisesti se ei käytä kuvan lukumäärää.

Anna olla Abc On suorakaiteen muotoinen kolmio, jossa on suora kulma C.. Viettää korkeus C. ja merkitse sen perustan H.. Kolmio ACH. Kuin kolmio Abc kahdella kulmalla. Vastaavasti kolmio Cbh Kuten Abc. Nimitysten syöttäminen

vastaanottaa

Mikä on vastaava

Taitettava, saada

Todiste avaruudesta menetelmällä

Alla näyttöä huolimatta näennäisestä yksinkertaisuudesta ei ole niin yksinkertaista. Kaikki heistä käyttävät alueen ominaisuuksia, jotka todisteet ovat monimutkaisempia todisteena pythagoran teoremista.

Todiste EquOdoplotibility

1. Aseta neljä yhtä suurta suorakulmaista kolmiota kuvion 1 mukaisesti.
2. Quadriili sivuilla c. Se on neliö, koska kahden terävän 90 ° kulman summa ja laajennuskulma on 180 °.
3. Koko luku on yhtä kuin toisaalta neliön neliö sivulla (A + B) ja toisaalta neljän kolmiojen ja kahden sisäisen neliön alueiden summa.

Q.E.D.

Todisteita Equivafusion kautta

Elegantti todiste permutaatiosta

Esimerkki yhdestä tällaisesta todisteista on määritelty oikealla olevassa piirustuksessa, jossa hypotenuusin sisäänrakennettu neliö on muunnettu kahteen ruutuun, joka on rakennettu katteihin.

TODISTUS EUCLIDEAN

Piirustus todisteisiin euklide

Kuva euklidean todisteeksi

Todisteita koskeva ajatus on seuraava: Yritetään todistaa, että hypotenuussa rakennetun neliön neliön puolet on yhtä suuri kuin puolet neliöt, jotka on rakennettu katteihin, ja sitten suuri ja suuri ja suuri Kaksi pientä neliötä ovat yhtä suuret.

Harkitse piirustusta vasemmalle. Siellä rakennettiin neliöt suorakulmaisen kolmion sivuilla ja suoritetaan suoran kulman kärkillä, kun säde on kohtisuorassa AB-hypotenyy, se erottaa hypotenuusi, kaksi suorakulmiota - BHJI ja Hakj , vastaavasti. On osoittautunut, että suorakulmaisten datan alue on täsmälleen yhtä suuri kuin vastaaviin luokkiin rakennetut neliöt.

Yritämme todistaa, että DECA-neliön neliö on yhtä suuri kuin suorakulmion Ahjk alue, jota käytämme apuarvosta: kolmio, jolla on sama korkeus ja syy, koska tämä suorakulmio on yhtä suuri kuin puolet määritetyn suorakulmion alueelta. Tämä on seurausta kolmiopin alueen määrittämisestä puoliksi pohjan tuotteesta korkeuteen. Tästä havainnosta seuraa, että ACK-kolmion pinta-ala on yhtä suuri kuin AHK-kolmio (ei esitetty kuvassa), joka puolestaan \u200b\u200bon puolet Ahjk-suorakulmion alueesta.

Todistamme nyt, että ACK-kolmio-alue on myös puolet DECA-aukion neliöstä. Ainoa asia, joka on tehtävä, on todistaa ACK- ja BDA-kolmioiden tasa-arvo (koska BDA-kolmioalue on yhtä suuri kuin yllä olevan neliön neliö). Tasa-arvo on ilmeinen, kolmiot ovat yhtä kuin kaksi puolta ja niiden välinen kulma. Se on - AB \u003d AK, AD \u003d AC - CAK-kulmien tasa-arvo ja huono helppo todistaa liikkumismenetelmällä: Käännän kolmio CAK 90 ° vastapäivään, niin on selvää, että vastaavat osapuolet tarkasteltavana olevan kolmio Samaa (johtuen siitä, että neliön yläosassa oleva kulma - 90 °).

Perustelu BCFG-aukion neliön ja BHJI-suorakulmion tasa-arvosta on täysin samanlainen.

Näin ollen olemme osoittaneet, että hypotenuusin rakennetun neliön neliö koostuu katteihin rakennettujen neliöistä. Tämän todistuksen ajatusta kuvataan lisäksi edellä mainitulla animaatiolla.

Todistus Leonardo da Vinci

Todistus Leonardo da Vinci

Todistuksen tärkeimmät elementit - symmetria ja liike.

Harkitse piirustusta, kuten symmetriasta voidaan nähdä, leikataan C.I. leikkaa neliön A.B.H.J. kahdella identtisellä osalla (kolmioina) A.B.C. ja J.H.I. yhtä suuri kuin rakentaminen). Käyttämällä 90 astetta vastapäivään, näemme varjostettujen lukujen tasa-arvon C.A.J.I. ja G.D.A.B. . Nyt on selvää, että varjostettujen lukujen pinta-ala on yhtä suuri kuin puolet katteihin rakennettujen neliöiden neliöiden ja alkuperäisen kolmioon. Toisaalta se on yhtä suuri kuin hypotenuusin rakennetun neliön neliö sekä alkuperäisen kolmion alue. Viimeinen vaihe todisteessa annetaan lukijalle.

Todiste on äärettömän pieni

Seuraavat todisteet erotusyhtälöiden avulla johtuvat usein kuuluisasta englantilaisesta matematiikasta, joka asui 1900-luvun alkupuoliskolla.

Ottaen huomioon kuvassa esitetyn piirustuksen ja muutoksen katseleminen a.Voimme tallentaa seuraavan suhdetta äärettömän pienille osapuolille peräkkäin ja a. (Trianglesin samankaltaisuuden käyttäminen):

Todiste on äärettömän pieni

Käyttämällä muuttujien erotusmenetelmää löydämme

Yleisempi ilmaisu hypotenuesin muuttamiseksi molempien kategorioiden välein

Tämän yhtälön integrointi ja alkuperäisten olosuhteiden avulla saamme

c. 2 = a. 2 + b. 2 + vakio.

Joten tulemme haluttuun vastaukseen

c. 2 = a. 2 + b. 2 .

Koska on helppo nähdä, lopullisen kaavan kvadraattinen riippuvuus näyttää kolmioon ja välein välisen lineaarisen suhteellisuuden vuoksi, kun taas määrä liittyy eri katetesien lisäyksestä.

Yksinkertaisempi todiste voidaan saada, jos oletamme, että yksi katetoksesta ei koe välein (tässä tapauksessa rullat b. ). Sitten integraatiovahtava

Muutokset ja yleistykset

• Jos on olemassa muita vastaavia lukuja ruudujen sijasta, ja Pythagora-teoreen yleistaminen on totta: Suorakulmaisessa kolmiossa katteihin rakennettujen kuvien summa on yhtä suuri kuin hypotenuusin rakennetun kuvan alue. Erityisesti:
  • Katteihin rakennettujen oikeiden kolmioiden määrä on yhtä suuri kuin oikean kolmioon, joka on rakennettu hypotenuusiin.
  • Kaateisiin rakennettujen puoliympyrän (kuten halkaisijaltaan) on yhtä suuri kuin hypotenuusin rakennettu puoliympyrän pinta-ala. Tätä esimerkkiä käytetään todisteena kahden ympyrän kaarien rajoittamien lukujen ominaisuuksista ja hypokraattisen vaahdon nimet.

Historia

Chu-Pey 500-200 BC. Vasemmalla merkinnällä: Korkeuden ja pohjapituuksien neliöiden summa on hypotenuusin pituuden neliö.

Muinaisessa kiinalaisessa kirjassa Chu-Pei puhuu Pythagoran kolmiosta osapuolten kanssa 3, 4 ja 5: Piirustus ehdotetaan samassa kirjassa, joka vastaa yhtä Basharan hindu-geometrian piirustuksista.

Cantor (suurin saksalainen historioitsija matematiikka) uskoo, että tasa-arvo 3 ² + 4 ² \u003d 5 ² jo egyptiläiset tunnetaan noin 2300 eKr. ER, Tsar Amen Inn I (Berliinin museon Papyrus 6619 mukaan). Mukaan Kantor, Harphedonapti, tai "köyden kiristimet" rakensivat suorit kulmat suorakulmaisilla kolmioilla osapuolten kanssa 3, 4 ja 5.

On erittäin helppo kopioida rakentamisen tapa. Ota köysi, jonka pituus on 12 m. Ja meidät sidotaan siihen värillisellä nauhalla 3 metrin etäisyydellä. Toisesta päästä ja 4 metrin päässä toisesta. Suorakulma tehdään osapuolten välillä 3 ja 4 metriä pitkään. Harpetonapitam voitaisiin väittää, että niiden rakentaminen muuttuu tarpeettomaksi, jos käytät esimerkiksi puupenkillä, jota kaikki puuseppä. Ja todellakin egyptiläiset piirustukset tunnetaan, joihin tällainen työkalu löytyy, kuten piirustukset, jotka kuvaavat puusepän työpajaa.

Jotkut ovat tietoisia Pythagoran teoremista Babylonian. Yhdessä tekstissä, joka johtuu Hammurabille, eli vuoteen 2000 eKr e. Suorakulmaisen kolmion hypotonuksen likimääräinen laskenta annetaan. Täältä voidaan päätellä, että kahden alueen pystyivät tekemään laskelmat suorakulmaisilla kolmioilla ainakin joissakin tapauksissa. Toisaalta nykypäivän tietämyksen taso Egyptin ja Babylonian matematiikan ja toisaalta kreikkalaisten lähteiden kriittisessä tutkimuksessa Van der Varden (Hollannin matemaatikko) teki seuraavan johtopäätöksen:

Kirjallisuus

Venäjäksi

• SKOBC Z. A. Geometriset miniatyyrit. M., 1990.
• Egniansky shch Pythagoran jalanjäljissä. M., 1961.
• Van der Varden B. L. Awakening tiedettä. Muinaisen Egyptin matematiikka, Babylon ja Kreikka. M., 1959.
• Glaser G. I. Matematiikan historia koulussa. M., 1982.
• V.Litzman, "Pytagora Theorem" M., 1960.
  • Sivusto Pythagore teoremista, jossa on suuri määrä todisteita, materiaali otetaan V.Littsmanin kirjasta, suuri määrä piirustuksia on edustettuna erillisinä graafisina tiedostoina.
• Pythagoran ja Pythagoran troikan teoreen The Book D. V. Anosov "Katso matematiikkaa ja jotain siitä"
• Pythagoreo Theorem ja todisteiden lasin, Academian Rao, Moskova

Englanniksi

• Pythagora Theorem wolframathworld (englanti)
• Cut-the-solmu, Pythagoran teoreen omistettu osa, noin 70 todisteita ja laaja lisätietoa (englanniksi)

Wikimedia-säätiö. 2010.

(Berliinin museon Papyruksen 6619 mukaan). Mukaan Cantor, HarphedonaPt, tai "köyden tiukemmat" rakensivat suorit kulmat suorakulmaisilla kolmioilla sivuilla 3, 4 ja 5.

On erittäin helppo kopioida rakentamisen tapa. Ota köysi pituus 12 m ja kiinnittää siihen värilliselle nauhalla 3 metrin etäisyydellä toisesta päästä ja 4 metrin päässä toisesta. Suorakulma päätetään osapuolten pituudelta 3 ja 4 metriä. Harpedonapitam voitaisiin väittää, että niiden rakentamismalli muuttuu tarpeettomaksi, jos käytät esimerkiksi kaikkien puusepän puinen hiili. Ja todellakin egyptiläiset piirustukset tunnetaan, joihin tällainen työkalu löytyy - esimerkiksi piirustukset, jotka kuvaavat puusepäntyöstöpajaa.

Jotkut ovat tietoisia Pythagoran teoremista Babylonian. Yhdessä tekstissä, joka johtuu Hammurapille, eli vuoteen 2000 mennessä BC. e. , Likimääräinen laskenta suorakaiteen muotoinen kolmio. Täältä voidaan päätellä, että kahden alueen pystyivät tekemään laskelmat suorakulmaisilla kolmioilla ainakin joissakin tapauksissa. Toisaalta nykypäivän tietämyksen taso Egyptin ja Babylonian matematiikan ja toisaalta kreikkalaisten lähteiden kriittisessä tutkimuksessa Van der Warden (Alankomaiden matemaatikko) totesi, että hypotenuusin neliön teorea oli tiedossa Intia on noin 1800-luvun BC. e.

Noin 400 eKr. E. Koettimen mukaan Platon antoi menetelmän Pythagora Trokin löytämiseksi, yhdistämällä algebra ja geometria. Noin 300 eKr e. "Euclidean" alussa Pythagoreo Theoremin vanhin aksiomaattinen todiste ilmestyi.

Muotoilu

Geometrinen sanamuoto:

Aluksi teorema formuloitiin seuraavasti:

Algebrallinen sanamuoto:

Toisin sanoen merkitsee kolmion hypotenuusin pituutta ja katetujen pituuden ja:

Molemmat sanamuodat ovat vastaavia, mutta toinen sanamuoto on alkeisempaa, se ei vaadi alueen käsitettä. Toisin sanoen toinen lausunto voidaan tarkistaa, mikään ei tiedä alueesta ja mittaa vain suorakulmion kolmiojen pituus.

Pythagoran Reverse Theorem:

Todiste jstk

Tällä hetkellä 367 näyttöä tästä teoremista kirjattiin tieteelliseen kirjallisuuteen. Todennäköisesti Pythagora Theorem on ainoa teorea, jolla on niin vaikuttava määrä todisteita. Tällainen lajike voidaan selittää vain geometrian teorian perustavanlaatuisella arvolla.

Tietenkin se on käsitteellisesti niitä voidaan jakaa pieneen määrään luokkia. Tunnetuin: Todisteet avaruusmenetelmällä, aksiomaattisella ja eksoottisella todisteilla (esimerkiksi differentiaaliyhtälöillä).

Tällaisten kolmioiden kautta

Seuraava todistus algebraalisesta sanamuodosta on yksinkertaisin näyttöön käynnissä suoraan aksiomista. Erityisesti se ei käytä kuvan lukumäärää.

Anna olla Abc On suorakaiteen muotoinen kolmio, jossa on suora kulma C.. Viettää korkeus C. ja merkitse sen perustan H.. Kolmio ACH. Kuin kolmio Abc kahdella kulmalla. Vastaavasti kolmio Cbh Kuten Abc. Nimitysten syöttäminen

vastaanottaa

Mikä on vastaava

Taitettava, saada

mitä vaadittiin todistaa

Todiste avaruudesta menetelmällä

Alla näyttöä huolimatta näennäisestä yksinkertaisuudesta ei ole niin yksinkertaista. Kaikki heistä käyttävät alueen ominaisuuksia, jotka todisteet ovat monimutkaisempia todisteena pythagoran teoremista.

Todiste EquOdoplotibility

1. Aseta neljä yhtä suurta suorakulmaista kolmiota kuvion 1 mukaisesti.
2. Quadriili sivuilla c. Se on neliö, koska kahden terävän 90 ° kulman summa ja laajennuskulma on 180 °.
3. Koko luku on yhtä kuin toisaalta neliön neliö sivulla (A + B) ja toisaalta neljä kolmiota ja sisäistä neliöaluetta .

Q.E.D.

TODISTUS EUCLIDEAN

Todisteita koskeva ajatus on seuraava: Yritetään todistaa, että hypotenuussa rakennetun neliön neliön puolet on yhtä suuri kuin puolet neliöt, jotka on rakennettu katteihin, ja sitten suuri ja suuri ja suuri Kaksi pientä neliötä ovat yhtä suuret.

Harkitse piirustusta vasemmalle. Siellä rakennettiin neliöt suorakulmaisen kolmion sivuilla ja suoritetaan suoran kulman kärkillä, kun säde on kohtisuorassa AB-hypotenyy, se erottaa hypotenuusi, kaksi suorakulmiota - BHJI ja Hakj , vastaavasti. On osoittautunut, että suorakulmaisten datan alue on täsmälleen yhtä suuri kuin vastaaviin luokkiin rakennetut neliöt.

Yritämme todistaa, että DECA-neliön neliö on yhtä suuri kuin suorakulmion Ahjk alue, jota käytämme apuarvosta: kolmio, jolla on sama korkeus ja syy, koska tämä suorakulmio on yhtä suuri kuin puolet määritetyn suorakulmion alueelta. Tämä on seurausta kolmiopin alueen määrittämisestä puoliksi pohjan tuotteesta korkeuteen. Tästä havainnosta seuraa, että ACK-kolmion pinta-ala on yhtä suuri kuin AHK-kolmio (ei esitetty kuvassa), joka puolestaan \u200b\u200bon puolet Ahjk-suorakulmion alueesta.

Todistamme nyt, että ACK-kolmio-alue on myös puolet DECA-aukion neliöstä. Ainoa asia, joka on tehtävä, on todistaa ACK- ja BDA-kolmioiden tasa-arvo (koska BDA-kolmioalue on yhtä suuri kuin yllä olevan neliön neliö). Tasa-arvo on ilmeinen: kolmiot ovat yhtä kuin kaksi puolta ja niiden välinen kulma. Se on - AB \u003d AK, AD \u003d AC - CAK-kulmien tasa-arvo ja huono helppo todistaa liikkumismenetelmällä: Käännän kolmio CAK 90 ° vastapäivään, niin on selvää, että vastaavat osapuolet tarkasteltavana olevan kolmio Samaa (johtuen siitä, että neliön yläosassa oleva kulma - 90 °).

Perustelu BCFG-aukion neliön ja BHJI-suorakulmion tasa-arvosta on täysin samanlainen.

Näin ollen olemme osoittaneet, että hypotenuusin rakennetun neliön neliö koostuu katteihin rakennettujen neliöistä. Tämän todistuksen ajatusta kuvataan lisäksi edellä mainitulla animaatiolla.

Todistus Leonardo da Vinci

Todistuksen tärkeimmät elementit - symmetria ja liike.

Harkitse piirustusta, kuten symmetriasta nähdään, segmentti hajottaa neliön kahteen identtiseen osaan (kolmioina ja ovat yhtä suuria kuin rakentaminen).

Käyttämällä kääntämällä 90 astetta vastapäivään nähden, näemme varjostettujen lukujen tasa-arvon ja.

Nyt on selvää, että varjostettujen lukujen pinta-ala on yhtä suuri kuin puolet pienten neliöiden (rakennettu katteihin) ja lähde kolmiskon alue. Toisaalta se on puolet suuren neliön neliöstä (sisäänrakennettu hypotense) sekä lähde kolmio-alue. Siten puolet pienten neliöiden neliöiden summasta on puolet suuren neliön alueesta, ja siksi katteihin rakennettujen neliöiden neliöiden summa on yhtä suuri kuin hypotenuussa rakennetun neliön neliö .

Todiste on äärettömän pieni

Seuraavat todisteet erotusyhtälöiden avulla johtuvat usein kuuluisasta englantilaisesta matematiikasta, joka asui 1900-luvun alkupuoliskolla.

Ottaen huomioon kuvassa esitetyn piirustuksen ja muutoksen katseleminen a.Voimme tallentaa seuraavan suhdetta äärettömän pienille osapuolille peräkkäin ja a. (Trianglesin samankaltaisuuden käyttäminen):

Käyttämällä muuttujien erotusmenetelmää löydämme

Yleisempi ilmaisu hypotenuesin muuttamiseksi molempien kategorioiden välein

Tämän yhtälön integrointi ja alkuperäisten olosuhteiden avulla saamme

Joten tulemme haluttuun vastaukseen

Koska on helppo nähdä, lopullisen kaavan kvadraattinen riippuvuus näyttää kolmioon ja välein välisen lineaarisen suhteellisuuden vuoksi, kun taas määrä liittyy eri katetesien lisäyksestä.

Yksinkertaisempi todiste voidaan saada, jos oletamme, että yksi katetoksesta ei koe lisäys (tässä tapauksessa Catat). Sitten integraatiovahtava

Muutokset ja yleistykset

Samankaltaiset geometriset muodot kolmella puolella

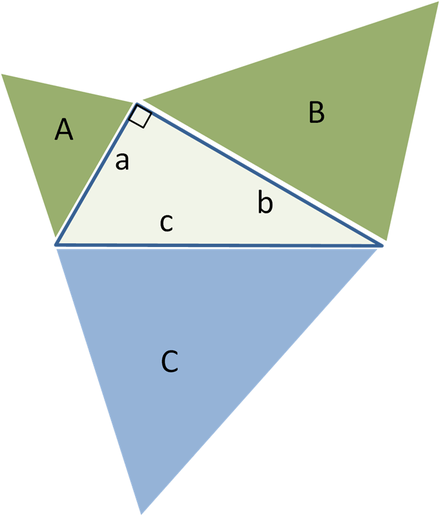
Vastaavien kolmioiden yleistys, vihreiden kuvioiden alue A + B \u003d neliö sininen C

Pythagoren teoria käyttäen samanlaisia \u200b\u200bsuorakulmaisia \u200b\u200bkolmioita

Pythagoran teoreen yleistyminen teki euklidin työstään alkaa, laajentaa neliöiden neliöitä sivuilla tällaisten geometristen muotojen alueille:

Jos rakennat samanlaisia \u200b\u200bgeometrisiä muotoja (ks. Euklidean geometria) suorakulmaisen kolmion sivuilla, kahden pienemmän kuvion summa on yhtä suuri kuin suurempi muoto.

Tämän yleistymisen pääajatus on se, että tällaisen geometrisen muodon alue on verrannollinen minkä tahansa lineaarisen koon neliöön ja erityisesti minkä tahansa sivun pituuden neliöön. Näin ollen samanlaisille muodoille neliöt A., B. ja C. rakennettu sivuilla pitkällä a., b. ja c.Meillä on:

Mutta Pythagora teoremin mukaan, a. 2 + b. 2 = c. 2, sitten A. + B. = C..

Ja päinvastoin, jos voimme todistaa sen A. + B. = C. Kolme samankaltaista geometrista kuvaa käyttämättä Pythagoren teoriaa, voimme todistaa itse teoremiksi, liikkua vastakkaiseen suuntaan. Esimerkiksi aloituskeskuskolmio voidaan käyttää uudelleen kolmiona C. Hypotenuusista ja kaksi samankaltaista suorakulmaista kolmiota ( A. ja B.), rakennettu kahteen muuhun osapuoleen, jotka on muodostettu sen korkeuden keskipisteen jakamisesta. Kahden pienemmän kolmiosaan summa on ilmeisesti yhtä suuri kuin kolmasosa, joten A. + B. = C. Ja suorittamalla edellinen todistettu päinvastaisessa järjestyksessä saamme pythagoran teoremin A 2 + B 2 \u003d C2.

Kosinus theorem

Pythagoreo-lause on erityinen tapaus yleisempi kosoaineita, joka sitoo osapuolten pituudet mielivaltaisessa kolmessa:

jossa θ on osapuolten välinen kulma a. ja b..

Jos θ on 90 astetta, sitten cos θ \u003d 0 ja kaava yksinkertaistetaan tavalliselle Pythagoreo-teoreelle.

Mielivaltainen kolmio

Kaikissa valittuun kulmaan mielivaltainen kolmio osapuolten kanssa a, B, C Suoritamme erinomaisen kolmion siten, että sen peruskulmut emäksessä ovat yhtä suuret kuin valittu kulma. Oletetaan, että valittu kulma θ sijaitsee vastapäätä sitä sivua c.. Tämän seurauksena saimme ABD-kolmio, jossa on kulma θ, joka sijaitsee vastapäätä osapuolia a. ja sivu r.. Toinen kolmio on muodostettu kulma θ, joka sijaitsee vastapäätä osapuolia b. ja sivu peräkkäin Lena s., kun se näkyy kuvassa. Sabit Ibn Kurra väitti, että näissä kolmessa kolmikulmiossa olevat osapuolet liittyvät seuraavat:

Kun kulma θ lähestyy π / 2, epätarkastuneen kolmiojen pohja pienenee ja R: n kaksi puolta päällekkäin toisiaan vähemmän. Kun θ \u003d π / 2, ADB kääntyy suorakaiteen muotoiseksi kolmioksi, r. + s. = c. Ja saamme Pythagoran alkuperäisen teoreen.

Harkitse yhtä argumentteja. ABC-kolmiossa on samat kulmat kuin ABD Triangle, mutta päinvastaisessa järjestyksessä. (Kaksi kolmiota on yhteinen kulma B: n yläosassa, molemmilla on kulma θ ja niillä on myös sama kolmas kulma kolmion kulmien määrällä), vastaavasti ABC on samanlainen kuin ABD DBA-kolmion heijastus, kuten on esitetty alemmassa kuvassa. Me kirjoitamme vastakkaisten sivujen ja kulman viereen suhde,

Myös toisen kolmioon,

Siirrä fraktiot ja lisää nämä kaksi suhdetta:

q.E.D.

Yleistys mielivaltaisten kolmioiden kautta rinnakkaiseiden kautta

Yleismyynti mielivaltaisiin kolmioihin
Neliön vihreä tontti \u003d neliö Pyhimys

Todiste siitä, että edellä kuvatussa kuvassa

Yleisömme edelleen epäsuoria kolmioita käyttäen rinnakkaispolttoaineita kolmella puolella neliöiden sijasta. (neliöt - erityinen tapaus.) Yläkuva osoittaa, että akuutin kolmioon pitkän puolen suuntainen rinnakkaisalue on yhtä suuri kuin yhden muun sivun rinnakkaisarvo, edellyttäen, että pitkän puolen rinnakkaisrakenne on rakennettu, kuten on esitetty Kuviossa (nuolilla merkityt mitat ovat samoja ja määritellyt sivut alemman rinnakkaisuuden). Tämä yhdensuuntaisten rinnakkaisten neliöiden korvaaminen on selkeä samankaltaisuus alkuperäisen Pythagoran teoreen kanssa, uskotaan, että se oli formuloitu alexandrian PAP: ssä 4 g. e.

Alempi piirustus näyttää todistuskurssin. Katsotaanpa kolmioon vasemmalle puolelle. Vasen vihreällä rinnakkaisella on sama alue kuin sinisen rinnakkain, koska niillä on sama pohja. b. ja korkeus h.. Lisäksi vasemmalla vihreällä rinnakkaisella on sama alue kuin vasemman vihreän rinnakkain yläosassa, koska niillä on yhteinen pohja (kolmion vasemmassa yläkulmassa) ja kokonaiskorkeus kohtisuoraan kolmion puolelle. Samoin väitetään kolmioon oikealla puolella todistamme, että alempi rinnakkaisella on sama alue kuin kahdessa vihreässä rinnakkaisessa.

Monimutkaiset numerot

Pythagoren teoremia käytetään etsimään kahden pisteen välistä etäisyyttä Cartesian koordinaattijärjestelmässä, ja tämä teorema on voimassa kaikille todellisille koordinaateille: etäisyys s. kahden pisteen välillä ( a, B.) ja ( c, D.) Yhtä suuri

Kaavan kanssa ei ole ongelmia, jos he kohtelevat monimutkaisia \u200b\u200bnumeroita vektoreina, joissa on voimassa olevat komponentit x. + i y. = (x., y.). . Esimerkiksi etäisyys s. välillä 0 + 1 i. ja 1 + 0 i. Laske Vector-moduulina (0, 1) − (1, 0) = (−1, 1), tai

Monimutkaisilla koordinaateilla tehdyillä toiminnalla on kuitenkin välttämätöntä suorittaa tietty parannusta Pythagoran kaavan. Etäisyys pisteiden välillä monimutkaisilla numeroilla ( a., b.) ja ( c., d.); a., b., c., I. d. Kaikki monimutkainen, formulaat käyttävät absoluuttisia arvoja. Etäisyys s. Perustuu vektoriero (a. − c., b. − d.) Seuraavassa muodossa: anna ero a. − c. = p. + I. q.missä p. - todellinen osa eroa, q. - kuvitteellinen osa ja i \u003d √ (-1). Samoin anna sen b. − d. = r. + I. s.. Sitten:

missä on monimutkainen konjugaattinumero. Esimerkiksi pisteiden välinen etäisyys (a., b.) = (0, 1) ja (c., d.) = (i., 0) , Laske ero (a. − c., b. − d.) = (−i., 1) Ja tämän seurauksena saisimme 0, jos monimutkaisia \u200b\u200bkonjugaatteja ei käytetty. Näin ollen parannetun kaavan avulla saamme

Moduuli määritellään seuraavasti:

Stereometria

Pythagoran teoreen merkittävä yleistys kolmiulotteiselle tilalle on de Gua-teorea, jonka nimi on Z.-P. De Gua: Jos Tetrahedronilla on suora kulma (kuten Kuubassa), kasvojen alueen neliö, joka sijaitsee vastapäätä suorakulmaa, on yhtä kuin kolmen alueen neliöiden summa kasvot. Tämä johtopäätös voidaan yleistää " n.-Mimaal Pythagore Theorem ":

Pythagoren lause kolmiulotteisessa tilassa yhdistää mainosten diagonaalin kolmella osapuolella.

Muu yleistyminen: Pythagoreo Theorem voidaan levittää stereometriaan seuraavassa muodossa. Harkitse suorakaiteen muotoisuutta, kuten kuviossa on esitetty. Löydä Pythagoran teoremin diagonaalisen BD: n pituus:

jossa kolme puolta muodostavat suorakulmainen kolmio. Käytämme BD: n vaakasuoraa diagonaalia ja AB: n pystysuoran reunan löytämiseksi mainostodistuksen pituuden, sillä tämä uudelleen käyttää Pythagoren teoriaa:

tai jos he kirjoittavat kaiken yhdessä yhtälössä:

Tämä tulos on kolmiulotteinen ilmaus vektorin suuruuden määrittämiseksi v. (Diagonaalinen mainos) ilmaistuna kohtisuorassa komponenttien ( v. k) (kolme keskenään kohtisuorassa sivua):

Tätä yhtälöä voidaan pitää Pythagoran teoreen yleismäksi moniulotteiselle tilalle. Tuloksessa ei kuitenkaan ole mitään muuta kuin Pythagoras-teoremin toistuva käyttö suorakulmaisten kolmiojen sekvenssiin johdonmukaisesti kohtisuorassa tasossa.

Vektoritila

Vektoreiden ortogonaalisen järjestelmän tapauksessa on myös tasa-arvo, jota kutsutaan myös pythagores teoreiksi:

Jos se on koordinaatti-akseleiden vektorin ulokkeet, tämä kaava vastaa Euklideusetäisyyden kanssa - ja tarkoittaa, että vektorin pituus on yhtä suuri kuin sen komponenttien neliöt.

Tämän tasa-arvon analoginen analoginen vektorien ääretön järjestelmä on yhdenvertaisen puolueiden nimeä.

Neevklidova Geometria

Pythagoreo-teorema on peräisin euklidean geometrian aksioomista ja itse asiassa ei ole kelvollinen ei-epätäydelliselle geometrialle, jossa muodossa on edellä oleva muoto. (Toisin sanoen, Pythagore lause osoittautuu eräänlainen vastaava euklidisen n postulaatin on rinnakkaisuus) toisin sanoen, ei-lapsi geometria, suhde kolmion sivut ovat välttämättä olla muodoltaan muu kuin Pythagoraan lauseen. Esimerkiksi pallomaisessa geometriassa kaikki kolme puolta suorakaiteen muotoinen kolmio (sano a., b. ja c.), joka rajoittuu yhdelle pallolle kahdeksankertaiseen osaan), on pituus π / 2, joka on ristiriidassa Pythagoran teoreen kanssa, koska a. 2 + b. 2 ≠ c. 2 .

Harkitse tässä kaksi tapausta kuin lapsen geometria - pallomaiset ja hyperboliset geometria; Molemmissa tapauksissa, kuten suorakulmaisten kolmioiden euklideantilaa varten, tulosta, joka korvaa pytagora-teoreen, seuraa kosinista teoremista.

Pythagoreo-lause on kuitenkin oikeudenmukainen hyperboliseen ja elliptiseen geometriaan, jos kolmion suorakulmioiden vaatimus korvataan sillä edellytyksellä, että kahden kolmiojen kulmien summa on yhtä suuri kuin kolmas, sanotaan A.+B. = C.. Sitten osapuolten välinen suhde näyttää tältä: ympyrät, joiden halkaisijat a. ja b. yhtä suuri kuin ympyrän pinta halkaisija c..

Pallomainen geometria

Mille tahansa suorakulmaiselle kolmiolle säteellä R. (Esimerkiksi, jos kulma γ linja kolmiossa) osapuolten kanssa a., b., c. Osapuolten välinen suhde on tällainen:

Tämä tasa-arvo voidaan johtaa erityisenä tapauksena pallomaisen kosini-teoreen, joka on voimassa kaikille pallomaisille kolmioille:

jossa cosh on hyperbolinen kosiini. Tämä kaava on erityinen hyperbolinen kosini-lause, joka on voimassa kaikille kolmioille:

jossa γ on kulma, jonka kärki on päinvastoin c..

missä g. iJ. nimeltään Metrinen tensor. Se voi olla sijaintitoiminto. Tällaisia \u200b\u200bkaarevia tiloihin kuuluvat Riemannian geometria yleisenä esimerkkinä. Tämä sanamuoto sopii myös euklideantilaan, kun käytetään kaarevia koordinaatteja. Esimerkiksi Polar-koordinaatit:

Vektovekniikka

Pythagoreo Theorem yhdistää kaksi ilmaisua vektorituotteen suuruudesta. Yksi vektorityön määritelmän lähestymistavoista edellyttää, että se täyttää yhtälön:

tämä kaava käyttää skalaarista tuotetta. Yhtälön oikealla puolella kutsutaan determinanttinen gramma a. ja b.Mikä on yhtä suuri kuin näiden kahden vektorin muodostaman rinnakkaispolku. Tämän vaatimuksen perusteella sekä vektorituotteen kohtisuorausvaatimukset sen osatekijälle a. ja b. Tästä seuraa, että 0 ja 1-ulotteisen tilan vähäpätöisten tapausten lukuun ottamatta vektorituote määritellään vain kolmessa ja seitsemässä ulottuvuudessa. Käytämme kulman määritelmää n.- Mittatila:

tämä vektorituotteen ominaisuus antaa arvonsa tässä muodossa:

Pythagoren perustavanlaatuisen trigonometrisen identiteetin kautta saamme toisen muodon sen arvon tallentamiseksi:

Vaihtoehtoinen lähestymistapa vektorituotteen määritelmään käyttää ilmaisua sen suuruusluokkaa. Sitten väitetään päinvastaisessa järjestyksessä, saamme suhdetta skalaarin tuotteeseen:

Katso myös

Toteaa

1. Historia Aihe: Pythagoras's Theorem Babylonian matematiikassa
2. (P. 351) P. 351
3. (, Vol i, s. 144)
4. Keskustelu historiallisista tosiasioista annetaan (, s. 351) P. 351
5. Kurt von Fritz (huhtikuu, 1945). "INPIPONTUMin HIPPOSUSUKSEN REMMMENFERY". Matematiikan, toisen sarjan Annals of Matematics) 46 (2): 242–264.
6. Lewis Carroll, "historia nodules", M., MIR, 1985, s. 7.
7. Asger AABOE. Episodit matematiikan varhaisesta historiasta. - Matemaattinen Amerikan yhdistys, 1997. - P. 51. - ISBN 0883856131
8. Pythagoran-ehdotus, ELISHA SCOTT LOOMIS
9. Euclidin. Elementit: Varaa VI, ehdotus VI 31: "Oikean kulmassa kolmiossa, joka on oikean kulman puolelta, on yhtä suuri kuin samanlainen ja vastaavasti kuvattu lukuja, jotka sisältävät oikean kulman."
10. Lawrence S. Leff. mainittu työ. . - Barronin koulutussarja. - P. 326. - ISBN 0764128922
11. Howard Whitley Eves. §4.8: ... Pythagoran teoremin yleistys // Matematiikan suuret hetket (ennen 1650). - Amerikan matemaattinen yhdistys, 1983. - P. 41. - ISBN 0883853108
12. Tâbit Ibn Qurra (täydellinen nimi Thābnin Ibn Qurra Ibn Marwan Al-ṣBI "Al-ḥarrānī (826-901 AD) oli Lääkäri, joka asuu Bagdadissa, joka kirjoitti laajasti euklidin elementteihin ja muihin matemaattisiin aiheisiin.
13. Aydin Sayli (1960 maaliskuu). "Thâbit Ibn Qurra" s yleistys Pythagoran teoremin ". Isis 51 (1): 35-37. DOI: 10.1086 / 348837.
14. Judith D. Sally, Paul Sally Harjoitus 2.10 (ii) // mainittu työ. - P. 62. - ISBN 0821844032
15. Katso tällaisen rakenteen yksityiskohdat George Jennings. Kuva 1.32: Yleinen Pythagoran teorem // moderni geometria, jossa on sovelluksia: 150 lukua. - Kolmas. - Springer, 1997. - P. 23. - ISBN 038794222x
16. Arlen Brown, Carl M. Pearcy Kohde. C.: Normi \u200b\u200bmielivaltaiseen n.-Tuple ... // Analyysi. - Springer, 1995. - P. 124. - ISBN 0387943692 Katso myös sivut 47-50.
17. Alfred Grey, Elsa Abbena, Simon Salamon Moderni differentiaalinen geometria, jossa on matemaattiset käyrät ja pinnat. - Kolmas. - CRC Press, 2006. - s. 194. - ISBN 1584884487
18. Rajendra Bhatia. Matrix-analyysi. - Springer, 1997. - P. 21. - ISBN 0387948465
19. Stephen W. Hawking mainittu työ. . - 2005. - P. 4. - ISBN 0762419229
20. Eric W. WEISEIN. CRC tiivistää matematiikan tietosanakirja. - 2.. - 2003. - P. 2147. - ISBN 1584883472
21. Alexander R. Pruss.

Pythagoraan lause - yksi euklidean geometrian perustavanlaatuisista teoreista

suorakulmaisen kolmion sivujen välillä.

Kreikan matemaatikko Pythagore uskotaan osoittamaan, mitkä ja nimetty.

Pythagoran teoremin geometrinen formulaatio.

Aluksi teorema formuloitiin seuraavasti:

Suorakulmaisessa kolmiossa hypotenuusin rakennetun neliön neliö on yhtä suuri kuin neliöiden neliöiden summa,

rakennettu katteihin.

Pythagoran teoremin algebrallinen formulaatio.

Suorakulmaisessa kolmiossa hypotenuusin pituuden neliö on yhtä suuri kuin kuljetuspituuden neliöiden summa.

Eli merkitsee kolmion hypotenuusin pituutta c.ja katetiden pituus a. ja b.:

Sekä sanamuoto pythagora Theoremsvastaava, mutta toinen sanamuoto on alkeisempaa, se ei ole

vaatii alueen käsitettä. Toisin sanoen toinen lausunto voidaan tarkistaa, mikään ei tiedä alueesta ja

mittaa vain suorakulmaisen kolmion sivujen pituus.

Pythagoran kääntää teorema.

Jos kolmio yhden puolen neliö on yhtä suuri kuin kahden muun sivun neliöiden summa, sitten

triangle on suorakulmainen.

Tai toisin sanoen:

Kaikki kolme positiivista numeroa a., b. ja c., näin

on olemassa suorakaiteen muotoinen kolmio tullilla a. ja b.ja hypotenuus c..

Pythagora teoremi vastikkeen kolmio.

Pythagoran teoremainen tasasivuinen kolmio.

Todiste Pythagoran teoremista.

Tällä hetkellä 367 näyttöä tästä teoremista kirjattiin tieteelliseen kirjallisuuteen. Luultavasti lause

Pythagora on ainoa teorea, jolla on niin vaikuttava määrä todisteita. Tällainen lajike

voidaan selittää vain geometrian teoremin perustavanlaatuisella arvolla.

Tietenkin se on käsitteellisesti niitä voidaan jakaa pieneen määrään luokkia. Tunnetuin niistä:

todiste jstk avaruusmenetelmä, aksiomaattinen ja eksoottiset todisteet (esimerkiksi,

kautta differentiaaliyhtälöt).

1. Todistus Pythagoren teoremasta tällaisten kolmioiden kautta.

Seuraavat todisteet algebraalisesta sanamuodosta ovat yksinkertaisin rakenteilla olevista todisteista.

suoraan aksiom. Erityisesti se ei käytä kuvan lukumäärää.

Anna olla Abc On suorakaiteen muotoinen kolmio, jossa on suora kulma C.. Viettää korkeus C. Ja merkitsee

sen perusta kautta H..

Kolmio ACH. Kuin kolmio AbC kahdelle kulmalle. Vastaavasti kolmio Cbh Kuten Abc.

Merkityksen syöttäminen:

saamme:

,

mikä vastaa -

Yhteensopiva a. 2 I. b. 2, saamme:

tai, mikä on tarpeen todistaa.

2. Todiste Pythagore teoremista alueen alueella.

Alla näyttöä huolimatta näennäisestä yksinkertaisuudesta ei ole niin yksinkertaista. Ne kaikki

käytä alueen ominaisuuksia, jotka todisteet ovat monimutkaisempia todisteena Pythagoran teoremasta.

• TODISTUS EQUODOCKAn kautta.

Aseta neljä yhtä suorakulmainen

triangle kuten kuvassa on esitetty

oikealla.

Quadriili sivuilla c. - neliö,

koska kahden terävän kulman summa, 90 ° ja

käytetty kulma - 180 °.

Koko luku on yhtä kuin yksi käsi,

neliöalue puolella ( a + B.), ja toisaalta neljä kolmiota ja

Q.E.D.

3. Todiste Pythagore teoremista menetelmän äärettömän pienen.

​

Ottaen huomioon kuviossa ja

tarkkailemalla sivun muutostaa., me voimme

kirjaa seuraava suhde ääretön

pieni sivun väleinperäkkäin ja a. (Käyttämällä semblace

triangles):

Käyttämällä muuttujan erotusmenetelmää löydämme:

Yleisempi ilmaisu hypotenuusin muuttamiseksi molempien kategorioiden välein:

Tämän yhtälön integrointi ja alkuperäisten olosuhteiden avulla saamme:

Siksi tulemme haluttuun vastaukseen:

Koska ei ole vaikea nähdä, lopullisen kaavan kvadraattinen riippuvuus näyttää lineaarisen

triansin sivujen ja välein välinen suhteellisuus, kun taas määrä liittyy itsenäiseen

talletukset eri katetiden lisäyksestä.

Yksinkertaisempi todiste voidaan saada, jos oletamme, että yksi katetoksesta ei koe lisäystä

(Tässä tapauksessa Catat b.). Sitten, kun integraatio vakio, saamme:

Keskitaso

Suorakulmainen kolmio. Täysi kuvitettu opas (2019)

SUORAKULMAINEN KOLMIO. ENSIMMÄINEN TASO.

Tehtävissä suorakulma ei ole lainkaan välttämätön - vasen pohja, joten sinun on opittava tunnistamaan suorakulmainen kolmio ja tässä muodossa,

ja niin

ja tässä

Mikä on hyvä suorakulmaisessa kolmion? No ... Ensinnäkin hänen puolinsa on erityisiä kauniita nimiä.

Huomiota piirustukseen!

Muista ja älä sekoita: kaksiteatteri - Kaksi ja hypotenuse - vain yksi (Ainoa, ainutlaatuinen ja pisin)!

No, nimet keskusteltiin, nyt tärkein asia: Pythagora teorem.

Pythagoraan lause.

Tämä teorema on avain monien tehtävien ratkaisemiseksi, kun osallistuminen suorakulmainen kolmio. Hän osoittautui Pythagoras täysin imememorial-aikoina, ja siitä lähtien hän on tuonut paljon hyödyllistä tietämystä. Ja paras asia on, että se on yksinkertainen.

Niin, Pythagoraan lause:

Muista vitsi: "Pythagoras housut kaikilla puolilla ovat yhtä suuret!"?

Piirrämme nämä Pythagoras-housut ja katsovat niitä.

Totta, se näyttää joitakin shortseja? No, mihin osapuoliin ja missä se on sama? Miksi ja missä vitsi tuli? Ja tämä vitsi on liitetty vain Pythagora-lauseesta, tarkemmin, kun Pythagore itse muotoiltiin teoreensa. Ja hän muotoili näin:

"Määrä neliöt neliötRakennettu katteihin yhtä suuri neliöeliöRakennettu hypotense. "

Totta, hieman erilainen ääni? Ja niin, kun Pythagoras kiinnitti teoreensa hyväksynnän, osoittautui juuri niin kuvaksi.

Tässä kuvassa pienten neliöiden määrä on yhtä suuri kuin suuren neliön neliö. Ja niin, että lapset muistuttavat paremmin, että kateton neliöiden summa on yhtä suuri kuin hypotenuusin neliö, joku nokkela ja keksin tämän vitun Pythagora housut.

Miksi olemme nyt muotoilemassa Pythagoren teorea

Ja Pythagoras kärsivät ja perustivat neliötä?

Näet, muinaisina aikoina ei ollut ... Algebras! Ei ollut merkitystä ja niin edelleen. Ei ole mitään merkintöjä. Kuvittelisit kuinka huono muinaiset opiskelijat olivat hirvittävän muistin kaikki sanat ??! Ja voimme nauttia siitä, että meillä on yksinkertainen formulaatio pythagores teorea. Toista se muistaa uudelleen:

Nyt sen pitäisi olla helposti:

Hypotenuusin neliö on yhtä suuri kuin kateton neliöiden summa.

No, tärkein teoremi, joka koskee suorakulmaista kolmiota. Jos olet kiinnostunut siitä, miten se osoittautui, lue seuraavat teorian tasot, ja nyt mennään edelleen ... Trigonometria! Sinuksen, Kosinuksen, tangentin ja koangenien kauheille sanoille.

Sinus, kosini, tangentti, kannetaan suorakulmaisessa kolmiossa.

Itse asiassa kaikki ei ole niin pelottavaa. Tietenkin "nykyinen" määritelmä sinus, kosini, tangentti ja opintojen on katsottava artikkelissa. Mutta en todellakaan halua, eikö? Voimme viitata: ratkaisemaan ongelmia suorakaiteen muotoinen kolmio, voit yksinkertaisesti täyttää seuraavat yksinkertaiset asiat:

Ja miksi se on vain kulmassa? Missä on kulma? Tämän vuoksi sinun on tiedettävä, miten lausunnot 1 - 4 kirjoittavat sanat. Katsokaa, ymmärrä ja muista!

1.
Yleensä se kuulostaa tästä:

Mikä on kulma? Onko olemassa CATT, joka on vastapäätä kulmaa, eli päinvastoin (nurkkaan) Katalat? Tietenkin on! Se on Cathe!

Mutta entä kulma? Katso huolellisesti. Mikä katti on kulman vieressä? Tietenkin Catat. Niin, Corner Catat - yksityisyys ja

Ja nyt huomiota! Katso, mitä teimme:

Katso kuinka viileä:

Nyt mennään tangenttiin ja Kotanceen.

Kuinka kirjoittaa tämä nyt? Katsomassa, mikä on suhteessa kulmaan? Vastapäätä, tietenkin hän "sijaitsee" vastapäätä nurkkaa. Ja Catat? Squirting nurkkaan. Joten mitä tapahtui meille?

Katso, numerointi ja nimittäjä muuttivat paikkoja?

Ja nyt taas kulmat ja vaihdettiin:

Yhteenveto

Kirjoitamme lyhyesti kaikki, mitä opimme.

Pythagoraan lause:

Tärkein teoreutti suorakaiteen muotoinen kolmio on pythagora teorem.

Pythagoraan lause

Muuten, muistatko hyvin, mitä katatenetit ja hypotenuus ovat? Jos ei oikeastaan, katsokaa piirtämistä - tuhoaa tietoa

On mahdollista, että olet jo käyttänyt Pythagoran teorea monta kertaa, mutta ajattelit, miksi tällainen teoremi on oikea. Kuinka todistaa se? Ja teemme niin muinaiset kreikkalaiset. Piirrä neliö sivuilla.

Katso kuinka Cunning jakoimme sen pituuksien leikkauksiin ja!

Ja nyt liitä merkityt kohdat

Täällä totuus huomasi myös jotain, mutta itse katsot piirustusta ja ajattele miksi niin.

Mikä on suuremman neliön alue? Oikea ,. Ja alue on pienempi? Varma, . Siellä pysyi neljän kulman kokonaispinta-alaa. Kuvittele, että otimme ne kaksi ja johti heidät toisiinsa hypotenuses. Mitä tapahtui? Kaksi suorakulmiota. Joten "leikkauksen" alue on yhtä suuri.

Kokeamme kaikki yhteen.

Muuntimme:

Joten vierailimme Pythagore - osoittivat sen teoremiksi muinaisella tavalla.

Suorakulmainen kolmio ja trigonometria

Suorakulmaiseen kolmioon suoritetaan seuraavat suhteet:

Akuutin kulman sininen on yhtä suuri kuin hypotenuusin vastakkaisen luokan asenne

Akuutin kulman kosini on yhtä suuri kuin vierekkäisen katteen asenne hypotenuusiksi.

Akuutin kulman tangentti on yhtä suuri kuin vastakkaisen katekanteen asenteen viereiseen kataaliin.

Akuutin kulman cotangenit ovat yhtä suuria kuin viereisen katteen asenne vastakkaiseen katetiin.

Ja jälleen kaikki tämä levyn muodossa:

Se on erittäin kätevä!

Merkkejä tasa-arvoista suorakulmaiset kolmiot

I. Kaksi luokkaa

II. Kateteella ja hypotense

III. Hypotenuusista ja akuutista kulmasta

IV. Cathetu ja akuutti kulmassa

a)

b)

Huomio! Tässä on erittäin tärkeää, että kartit ovat "merkityksellisiä". Esimerkiksi, jos se on näin:

Sitten kolmiot eivät ole yhtäläisiäHuolimatta siitä, että niillä on yksi identtinen akuutti kulma.

Tarvitsee Molemmissa kolmioissa Katalat olivat vierekkäin tai molemmissa päinvastoin.

Huomasitko, mitä suorakulmaisten kolmioiden tasa-arvoiset merkit eroavat kolmiojen tasa-arvon tavanomaisista merkkeistä? Aiheessa "ja kiinnitä huomiota siihen, että" tavallisten "kolmiojen tasa-arvo tarvitsee kolmen elementin tasa-arvoa: kaksi puolta ja kulmaa niiden välillä, kaksi kulmaa ja kolmen puolen välillä. Mutta suorakulmaisten kolmioiden tasa-arvosta vain kaksi vastaavaa elementtiä riittää. Suuri, eikö?

Suunnilleen sama tilanne ja merkkejä suorakulmaisten kolmioiden samankaltaisuudesta.

Merkkejä suorakulmaisten kolmioiden samankaltaisuudesta

I. Akuutti kulmassa

II. Kahdessa luokassa

III. Kateteella ja hypotense

Mediaani suorakulmaisessa kolmiossa

Miksi se on niin?

Harkitse suorakulmaista kolmiota koko suorakulmion.

Piirrämme diagonaalista ja harkita pistettä - diagonaalien leikkauspiste. Mitä tiedetään suorakulmion diagonaalista?

Ja mitä tästä seuraa?

Joten se osoittautui

1. - Mediana:

Muista tämä seikka! Auttaa paljon!

Ja se on vieläkin yllättävää, joten tämä on totta ja päinvastainen lausunto.

Mitä hyvää voidaan saada siitä, että hypotenuusiin käytetty mediaani on puolet hypotenyy? Ja katsotaanko kuvaa

Katso huolellisesti. Meillä on: toisin sanoen etäisyys siitä, että kolmesta kolmesta kolmesta pisteestä on osoittautuneet yhtäläiseksi. Mutta kolmiossa on vain yksi piste, etäisyys, josta kaikki kolme kolmiota on yhtä suuri, ja tämä on kuvattu ympyrä. Mitä tapahtui?

Täällä aloitetaan tällä "lisäksi ...".

Katsotaanpa ja.

Mutta tällaisissa kolmioissa kaikki kulmat ovat yhtä suuret!

Sama voidaan sanoa ja

Ja nyt minä vedän sen yhteen:

Millaista hyötyä voidaan oppia tästä "kolminkertaisesta" samankaltaisuudesta.

Esimerkiksi - Kaksi kaavaa suorakulmion kolmioon.

Kirjoitamme vastaavien osapuolten suhde:

Löytää korkeus ratkaisemme osuuden ja saada Ensimmäinen kaavan "korkeus suorakaiteen muotoisella kolmion":

Joten käytämme samankaltaisuutta :.

Mitä nyt tapahtuu?

Jälleen ratkaisemme osuuden ja saamme toisen kaavan:

Molemmissa näistä kaavojen on muistettava hyvin ja soveltaa sitä, joka on helpompaa. Me kirjoitamme ne uudelleen

Pythagoraan lause:

Suorakulmaisessa kolmiossa hypotenuusin neliö on yhtä suuri kuin katetesi neliöiden summa :.

Merkkejä suorakulmaisten kolmioiden tasa-arvosta:

• kahdessa luokassa:
• kateteella ja hypotense: tai
• kateteella ja viereisessä akuutissa kulmassa: tai
• katetu ja vastakkainen akuutti kulma: tai
• hypotense ja Akuutti kulmassa: Tai.

Suorakulmaisten kolmiojen samankaltaisuuden merkkejä:

• yksi akuutti kulma: tai
• kahden katean suhteellisuus:
• kaateisuuden ja hypoteningien suhteellisuudesta: Tai.

Sinus, kosini, tangentti, kanangainen suorakaiteen muotoisella kolmiossa

• Suorakulmaisen kolmion akuutin kulman sinea kutsutaan vastakkaisen luokan asenteeksi hypotenuse:
• Suorakulmaisen kolmion akuutin kulman kosinaa kutsutaan vierekkäisen luokan suhde hypotenuse:
• Suorakulmaisen kolmion terävän kulman tangentti kutsutaan vastakkaisen luokan asenteeksi viereiseen:
• Suorakulmaisen kolmion akuutin kulman kantonta kutsutaan viereisen luokan suhde päinvastoin :.

Suorakulmaisen kolmion korkeus: Tai.

Suorakulmaisessa kolmiossa suoran kulman kärsimyksestä suoritettu mediaani on puolet hypotenuse:

Suorakulmaisen kolmion alue:

• kissat: