How to find an acute angle between straight lines. Angle between straight lines on a plane

ANGLE BETWEEN THE PLANES

Consider two planes α 1 and α 2, given respectively by the equations:

Under angle between two planes we mean one of the dihedral angles formed by these planes. Obviously, the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or ... therefore ... Because and then

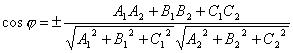Example. Determine the angle between planes x+2y-3z+ 4 \u003d 0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, which means .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or.

Thus, .

Examples.

STRAIGHT IN SPACE.

VECTOR LINE EQUATION.

PARAMETRIC EQUATIONS OF THE LINE

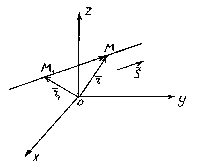
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding vector of this line.

So let it be straight l goes through the point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector.

Consider an arbitrary point M (x, y, z) on a straight line. The figure shows that .

Vectors and are collinear, so there is such a number t, what, where is the factor t can take any numerical value depending on the position of the point M on a straight line. Factor t called a parameter. Denoting the radius vectors of the points M 1 and M respectively, through and, we get. This equation is called vector equation of a straight line. It shows that for each value of the parameter t corresponds to the radius vector of some point Mlying on a straight line.

Let's write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric equations of a straight line.

When changing a parameter t coordinates change x, y and z and point M moves in a straight line.

CANONICAL EQUATIONS OF THE DIRECT

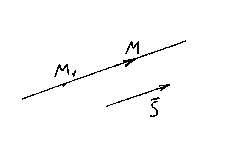
Let be M 1 (x 1 , y 1 , z 1) is a point lying on a straight line land Is its direction vector. Take again an arbitrary point on a straight line M (x, y, z) and consider a vector.

It is clear that vectors and are collinear, so their corresponding coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the straight line could be obtained from the parametric ones by excluding the parameter t... Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in parametric form.

We denote , from here x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the straight line be perpendicular to one of the coordinate axes, for example, the axis Ox... Then the directing vector is perpendicular Ox, Consequently, m\u003d 0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

However, in this case too, we agree to formally write the canonical equations of the straight line in the form ... Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox and Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS OF A LINE AS A LINE OF INTERSECTION OF TWO PLANES

An infinite number of planes pass through each straight line in space. Any two of them, intersecting, define it in space. Consequently, the equations of any two such planes, considered together, represent the equations of this straight line.

In general, any two non-parallel planes given by the general equations

define the line of their intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

To build a straight line, it is enough to find any two of its points. The easiest way is to select the intersection points of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of the straight line, setting z= 0:

Having solved this system, we find the point M 1 (1;2;0).

Similarly, setting y\u003d 0, we get the point of intersection of the straight line with the plane xOz:

From the general equations of a straight line, you can go to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 will be obtained from this system of equations by assigning an arbitrary value to one of the coordinates. To find the direction vector, note that this vector must be perpendicular to both normal vectors and ... Therefore, behind the direction vector of the straight line l we can take the cross product of normal vectors:

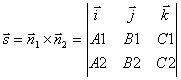Example. Give the general equations of the straight line to the canonical form.

Find a point lying on a straight line. To do this, we arbitrarily choose one of the coordinates, for example, y\u003d 0 and solve the system of equations:

Normal vectors of the planes defining the straight line have coordinates Therefore, the directing vector will be

... Consequently, l: .

ANGLE BETWEEN STRAIGHT

Corner between the straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle between the straight lines can be taken as the angle between their direction vectors and. Since, then, according to the formula for the cosine of the angle between the vectors, we get

I'll be brief. The angle between two lines is equal to the angle between their direction vectors. Thus, if you can find the coordinates of the direction vectors a \u003d (x 1; y 1; z 1) and b \u003d (x 2; y 2; z 2), you can find the angle. More precisely, the cosine of the angle by the formula:

Let's see how this formula works with specific examples:

A task. Points E and F are marked in the cube ABCDA 1 B 1 C 1 D 1 - the midpoints of edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AE and BF.

Since the edge of the cube is not indicated, we set AB \u003d 1. Introduce the standard coordinate system: the origin at point A, axes x, y, z are directed along AB, AD and AA 1, respectively. The unit segment is equal to AB \u003d 1. Now we find the coordinates of the direction vectors for our lines.

Find the coordinates of the vector AE. To do this, we need the points A \u003d (0; 0; 0) and E \u003d (0.5; 0; 1). Since point E is the midpoint of the segment A 1 B 1, its coordinates are equal to the arithmetic mean of the coordinates of the ends. Note that the origin of the vector AE coincides with the origin, so AE \u003d (0.5; 0; 1).

Now let's deal with the vector BF. Similarly, we parse the points B \u003d (1; 0; 0) and F \u003d (1; 0.5; 1), because F - midpoint of segment B 1 C 1. We have:
BF \u003d (1 - 1; 0.5 - 0; 1 - 0) \u003d (0; 0.5; 1).

So the direction vectors are ready. The cosine of the angle between straight lines is the cosine of the angle between the direction vectors, so we have:

A task. In a regular trihedral prism ABCA 1 B 1 C 1, all edges of which are equal to 1, points D and E are marked - the midpoints of edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AD and BE.

Let's introduce the standard coordinate system: the origin is at point A, the x axis is directed along AB, z - along AA 1. We direct the y-axis so that the OXY plane coincides with the ABC plane. The unit segment is equal to AB \u003d 1. Find the coordinates of the direction vectors for the sought lines.

First, let's find the coordinates of the AD vector. Consider the points: A \u003d (0; 0; 0) and D \u003d (0.5; 0; 1), because D - midpoint of segment A 1 B 1. Since the origin of the vector AD coincides with the origin, we obtain AD \u003d (0.5; 0; 1).

Now let's find the coordinates of the vector BE. Point B \u003d (1; 0; 0) is easy. With point E - the middle of the segment C 1 B 1 - it is a little more difficult. We have:

It remains to find the cosine of the angle:

A task. In a regular hexagonal prism ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, all edges of which are equal to 1, points K and L are marked - the midpoints of edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AK and BL.

Let us introduce a standard coordinate system for a prism: place the origin of coordinates in the center of the lower base, direct the x-axis along FC, the y-axis through the midpoints of the AB and DE segments, and the z-axis vertically upward. The unit segment is again equal to AB \u003d 1. Let's write out the coordinates of the points of interest to us:

Points K and L are the midpoints of segments A 1 B 1 and B 1 C 1, respectively, so their coordinates are found through the arithmetic mean. Knowing the points, we find the coordinates of the direction vectors AK and BL:

Now let's find the cosine of the angle:

A task. In the regular quadrangular pyramid SABCD, all edges of which are equal to 1, points E and F are marked - the midpoints of the sides SB and SC, respectively. Find the angle between lines AE and BF.

Let's introduce a standard coordinate system: the origin is at point A, the x and y axes are directed along AB and AD, respectively, and the z axis is directed vertically upward. The unit segment is equal to AB \u003d 1.

Points E and F are the midpoints of the segments SB and SC, respectively, so their coordinates are found as the arithmetic mean of the ends. Let's write out the coordinates of the points of interest to us:
A \u003d (0; 0; 0); B \u003d (1; 0; 0)

Knowing the points, we find the coordinates of the direction vectors AE and BF:

The coordinates of the vector AE coincide with the coordinates of the point E, since the point A is the origin. It remains to find the cosine of the angle:

Definition.If two straight lines y \u003d k 1 x + b 1, y \u003d k 2 x + b 2 are given, then the acute angle between these straight lines will be defined as

Two straight lines are parallel if k 1 \u003d k 2. Two straight lines are perpendicular if k 1 \u003d -1 / k 2.

Theorem.Straight lines Ax + Vy + C \u003d 0 and A 1 x + B 1 y + C 1 \u003d 0 are parallel when the proportional coefficients A 1 \u003d λA, B 1 \u003d λB. If also С 1 \u003d λС, then the lines coincide. The coordinates of the point of intersection of two straight lines are found as a solution to the system of equations of these straight lines.

Equation of a straight line passing through a given point

Perpendicular to this line

Definition.The straight line passing through the point M 1 (x 1, y 1) and perpendicular to the straight line y \u003d kx + b is represented by the equation:

Distance from point to line

Theorem.If a point M (x 0, y 0) is given, then the distance to the straight line Ax + Vy + C \u003d 0 is determined as

Evidence.Let point M 1 (x 1, y 1) be the base of the perpendicular dropped from point M onto a given straight line. Then the distance between points M and M 1:

(1)

The coordinates x 1 and y 1 can be found as a solution to the system of equations:

The second equation of the system is the equation of a straight line passing through a given point M 0 perpendicular to a given straight line. If we transform the first equation of the system to the form:

A (x - x 0) + B (y - y 0) + Ax 0 + By 0 + C \u003d 0,

then, solving, we get:

Substituting these expressions into equation (1), we find:

The theorem is proved.

Example... Determine the angle between the straight lines: y \u003d -3 x + 7; y \u003d 2 x + 1.

k 1 \u003d -3; k 2 \u003d 2; tgφ \u003d ; φ \u003d p / 4.

Example... Show that the straight lines 3x - 5y + 7 \u003d 0 and 10x + 6y - 3 \u003d 0 are perpendicular.

Decision... We find: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, therefore, the straight lines are perpendicular.

Example... The vertices of the triangle A (0; 1), B (6; 5), C (12; -1) are given. Find the equation for the height drawn from vertex C.

Decision... We find the equation of the side AB: ; 4 x \u003d 6 y - 6;

2 x - 3 y + 3 \u003d 0;

The required height equation is: Ax + By + C \u003d 0 or y \u003d kx + b. k \u003d. Then y \u003d. Because height passes through point C, then its coordinates satisfy this equation: whence b \u003d 17. Total:.

Answer: 3 x + 2 y - 34 \u003d 0.

Equation of a straight line passing through a given point in a given direction. Equation of a straight line passing through two given points. The angle between two straight lines. The condition of parallelism and perpendicularity of two lines. Determination of the intersection point of two lines

1. Equation of a straight line passing through a given point A(x 1 , y 1) in this direction, determined by the slope k,

y - y 1 = k(x - x 1). (1)

This equation defines a pencil of lines passing through the point A(x 1 , y 1), which is called the center of the beam.

2. Equation of a straight line passing through two points: A(x 1 , y 1) and B(x 2 , y 2) is written as follows:

The slope of a straight line passing through two given points is determined by the formula

3. Angle between straight lines A and B called the angle by which you need to turn the first straight A around the point of intersection of these lines counterclockwise until it coincides with the second line B... If two straight lines are given by equations with a slope

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

then the angle between them is determined by the formula

It should be noted that in the numerator of the fraction, the slope of the first straight line is subtracted from the slope of the second straight line.

If the equations of the straight line are given in general form

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

the angle between them is determined by the formula

4. Conditions for parallelism of two lines:

a) If the straight lines are given by equations (4) with a slope, then the necessary and sufficient condition for their parallelism consists in the equality of their slopes:

k 1 = k 2 . (8)

b) For the case when the straight lines are given by equations in general form (6), the necessary and sufficient condition for their parallelism is that the coefficients at the corresponding current coordinates in their equations are proportional, i.e.

5. Conditions of perpendicularity of two lines:

a) In the case when the straight lines are given by equations (4) with the slope, the necessary and sufficient condition for their perpendicularity is that their slopes are reciprocal in magnitude and opposite in sign, i.e.

This condition can also be written in the form

k 1 k 2 = -1. (11)

b) If the equations of straight lines are given in general form (6), then the condition for their perpendicularity (necessary and sufficient) is the fulfillment of the equality

A 1 A 2 + B 1 B 2 = 0. (12)

6. The coordinates of the point of intersection of two straight lines are found by solving the system of equations (6). Straight lines (6) intersect if and only if

1. Write the equations of the straight lines passing through the point M, one of which is parallel, and the other is perpendicular to a given line l.

OoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooTherefore, we will proceed to the first section, I hope that by the end of the article I will maintain a cheerful frame of mind.

The relative position of two straight lines

The case when the audience sings along with the chorus. Two straight lines can:

1) match;

2) be parallel:;

3) or intersect at a single point:.

Help for Dummies : please remember the mathematical sign of the intersection, it will be very common. The notation indicates that a straight line intersects a straight line at a point.

How to determine the relative position of two straight lines?

Let's start with the first case:

Two straight lines coincide if and only if their corresponding coefficients are proportional, that is, there is such a number "lambda" that the equalities

Consider straight lines and compose three equations from the corresponding coefficients:. It follows from each equation that, therefore, these lines coincide.

Indeed, if all the coefficients of the equation multiply by -1 (change signs), and all coefficients of the equation reduced by 2, you get the same equation:.

The second case, when the lines are parallel:

Two straight lines are parallel if and only if their coefficients for the variables are proportional: but.

As an example, consider two lines. We check the proportionality of the corresponding coefficients for the variables:

However, it is quite clear that.

And the third case, when the lines intersect:

Two straight lines intersect if and only if their coefficients for variables are NOT proportional, that is, there is NO such "lambda" value to make the equalities

So, for straight lines we will compose the system:

From the first equation it follows that, and from the second equation:, therefore, the system is inconsistent (no solutions). Thus, the coefficients of the variables are not proportional.

Conclusion: lines intersect

In practical problems, you can use the solution scheme just considered. By the way, it is very similar to the algorithm for checking vectors for collinearity, which we considered in the lesson The concept of linear (non) dependence of vectors. Vector basis... But there is a more civilized packaging:

Example 1

Find out the relative position of the straight lines:

Decision based on the study of direction vectors of straight lines:

a) From the equations we find the direction vectors of the straight lines: .

, so the vectors are not collinear and the lines intersect.

Just in case, I'll put a stone with pointers at the crossroads:

The rest jump over the stone and follow on, straight to Kashchei the Immortal \u003d)

b) Find the direction vectors of straight lines:

Lines have the same direction vector, which means that they are either parallel or coincide. There is no need to count the determinant here.

It is obvious that the coefficients for the unknowns are proportional, while.

Let us find out whether the equality is true:

Thus,

c) Find the direction vectors of straight lines:

Let us calculate the determinant composed of the coordinates of these vectors:
hence the direction vectors are collinear. Lines are either parallel or coincide.

The coefficient of proportionality "lambda" is easy to see directly from the ratio of collinear direction vectors. However, it can also be found through the coefficients of the equations themselves: .

Now let's find out if the equality is true. Both free terms are zero, so:

The resulting value satisfies this equation (any number generally satisfies it).

Thus, the lines coincide.

Answer:

Very soon you will learn (or even have already learned) to solve the considered problem orally in just a few seconds. In this regard, I see no reason to propose anything for an independent solution, it is better to lay another important brick in the geometric foundation:

How to build a straight line parallel to a given one?

For ignorance of this simplest task, the Nightingale the Robber severely punishes.

Example 2

The straight line is given by the equation. Equate a parallel line that goes through a point.

Decision: Let's denote the unknown direct letter. What does the condition say about her? The straight line goes through the point. And if the straight lines are parallel, then it is obvious that the directing vector of the straight line "tse" is also suitable for constructing the straight line "de".

We take out the direction vector from the equation:

Answer:

The geometry of the example looks simple:

Analytical verification consists of the following steps:

1) We check that the lines have the same direction vector (if the equation of the line is not simplified properly, then the vectors will be collinear).

2) Check if the point satisfies the obtained equation.

Analytical review is in most cases easy to do orally. Look at the two equations, and many of you will quickly determine the parallelism of straight lines without any drawing.

Examples for self-solution today will be creative. Because you still have to compete with Baba Yaga, and she, you know, is a lover of all kinds of riddles.

Example 3

Make an equation of a straight line passing through a point parallel to a straight line if

There is a rational and not very rational solution. The shortest way is at the end of the lesson.

We've done a bit of work with parallel lines and we'll come back to them later. The case of coinciding straight lines is of little interest, so consider a problem that is well known to you from the school curriculum:

How to find the intersection point of two lines?

If straight intersect at a point, then its coordinates are the solution systems of linear equations

How to find the point of intersection of lines? Solve the system.

So much for you geometric meaning of a system of two linear equations in two unknowns Are two intersecting (most often) straight lines on a plane.

Example 4

Find the point of intersection of lines

Decision: There are two ways of solving - graphical and analytical.

The graphical way is to simply draw the data lines and find out the intersection point directly from the drawing:

Here's our point:. To check it, you should substitute its coordinates in each equation of a straight line, they should fit both there and there. In other words, the coordinates of a point are the solution of the system. Basically, we looked at a graphical way to solve systems of linear equations with two equations, two unknowns.

The graphical method, of course, is not bad, but there are noticeable disadvantages. No, the point is not that seventh graders decide so, the point is that it will take time to get a correct and EXACT drawing. In addition, some straight lines are not so easy to construct, and the intersection point itself may be located somewhere in the thirty kingdom outside the notebook sheet.

Therefore, it is more expedient to look for the intersection point using the analytical method. Let's solve the system:

The method of term-by-term addition of equations was used to solve the system. Visit the lesson to develop relevant skills. How to solve a system of equations?

Answer:

The check is trivial - the coordinates of the intersection point must satisfy every equation in the system.

Example 5

Find the intersection point of the lines if they intersect.

This is an example for a do-it-yourself solution. It is convenient to divide the task into several stages. Analysis of the condition suggests what is needed:
1) Make the equation of the straight line.
2) Make the equation of the straight line.
3) Find out the relative position of the straight lines.
4) If the lines intersect, then find the intersection point.

The development of an algorithm of actions is typical for many geometric problems, and I will focus on this repeatedly.

Full solution and answer at the end of the tutorial:

A pair of shoes is not yet worn out, as we got to the second section of the lesson:

Perpendicular straight lines. Distance from point to line.
Angle between straight lines

Let's start with a typical and very important task. In the first part, we learned how to build a straight line parallel to this one, and now the hut on chicken legs will turn 90 degrees:

How to build a line perpendicular to a given one?

Example 6

The straight line is given by the equation. Equate a perpendicular line through a point.

Decision: By condition it is known that. It would be nice to find the direction vector of the straight line. Since the lines are perpendicular, the trick is simple:

From the equation "remove" the normal vector:, which will be the direction vector of the straight line.

Let us compose the equation of a straight line by a point and a direction vector:

Answer:

Let's expand the geometric sketch:

Hmmm ... Orange sky, orange sea, orange camel.

Analytical verification of the solution:

1) Take out the direction vectors from the equations and with the help dot product of vectors we come to the conclusion that the straight lines are indeed perpendicular:.

By the way, you can use normal vectors, it's even easier.

2) Check if the point satisfies the obtained equation .

The check is, again, easy to do orally.

Example 7

Find the point of intersection of perpendicular lines if the equation is known and point.

This is an example for a do-it-yourself solution. There are several actions in the task, so it is convenient to arrange the solution point by point.

Our exciting journey continues:

Distance from point to line

Before us is a straight strip of the river and our task is to reach it by the shortest route. There are no obstacles, and the most optimal route will be movement along the perpendicular. That is, the distance from a point to a straight line is the length of a perpendicular line.

Distance in geometry is traditionally denoted by the Greek letter "ro", for example: - the distance from the point "em" to the straight line "de".

Distance from point to line expressed by the formula

Example 8

Find the distance from point to line

Decision: all you need is to carefully plug the numbers into the formula and perform the calculations:

Answer:

Let's execute the drawing:

The distance from the point to the line found is exactly the length of the red line. If you draw up a drawing on checkered paper on a scale of 1 unit. \u003d 1 cm (2 cells), then the distance can be measured with an ordinary ruler.

Consider another task for the same blueprint:

The task is to find the coordinates of a point that is symmetrical to a point with respect to a straight line ... I propose to perform the actions yourself, but I will outline the solution algorithm with intermediate results:

1) Find a line that is perpendicular to the line.

2) Find the point of intersection of the lines: .

Both steps are detailed in this tutorial.

3) The point is the midpoint of the line segment. We know the coordinates of the middle and one of the ends. By formulas for the coordinates of the midpoint of the segment we find.

It will not be superfluous to check that the distance is also 2.2 units.

Difficulties here may arise in calculations, but in the tower, a micro calculator helps out great, allowing you to count ordinary fractions. Repeatedly advised, will advise and again.

How to find the distance between two parallel lines?

Example 9

Find the distance between two parallel lines

This is another example for an independent solution. Let me give you a little hint: there are infinitely many ways to solve it. Debriefing at the end of the lesson, but better try to guess for yourself, I think you managed to disperse your ingenuity quite well.

Angle between two straight lines

Every angle is a jamb:

In geometry, the angle between two straight lines is taken as the SMALLEST angle, which automatically implies that it cannot be obtuse. In the figure, the angle indicated by the red arc is not considered the angle between intersecting straight lines. And his "green" neighbor is considered as such, or oppositely oriented "Crimson" corner.

If the straight lines are perpendicular, then any of the 4 angles can be taken as the angle between them.

How do angles differ? Orientation. First, the direction of the corner "scrolling" is of fundamental importance. Second, a negatively oriented angle is written with a minus sign, for example, if.

Why did I tell this? It seems that you can do with the usual concept of an angle. The fact is that in the formulas by which we will find the angles, you can easily get a negative result, and this should not take you by surprise. An angle with a minus sign is no worse, and has a very specific geometric meaning. In the drawing, for a negative angle, be sure to indicate its orientation with an arrow (clockwise).

How to find the angle between two straight lines? There are two working formulas:

Example 10

Find the angle between straight lines

Decision and Method one

Consider two straight lines given by equations in general form:

If straight not perpendicularthen oriented the angle between them can be calculated using the formula:

Let's pay close attention to the denominator - this is exactly scalar product direction vectors of straight lines:

If, then the denominator of the formula vanishes, and the vectors will be orthogonal and the straight lines are perpendicular. That is why a reservation was made about the non-perpendicularity of the straight lines in the formulation.

Based on the above, it is convenient to arrange a solution in two steps:

1) Calculate the scalar product of the direction vectors of straight lines:
, therefore, the straight lines are not perpendicular.

2) The angle between the straight lines is found by the formula:

Using the inverse function, it is easy to find the corner itself. In this case, we use the oddness of the arctangent (see. Graphs and properties of elementary functions):

Answer:

In the answer, we indicate the exact value, as well as the approximate value (preferably both in degrees and in radians), calculated using a calculator.

Well, minus, so minus, that's okay. Here's a geometric illustration:

It is not surprising that the angle turned out to have a negative orientation, because in the problem statement, the first number is a straight line and the "twisting" of the angle began with it.

If you really want to get a positive angle, you need to swap the straight lines, that is, take the coefficients from the second equation , and the coefficients are taken from the first equation. In short, you must start with a straight line .

Instructions

note

The period of the trigonometric tangent function is 180 degrees, which means that the slope angles of the straight lines cannot, in absolute value, exceed this value.

Helpful advice

If the slopes are equal to each other, then the angle between such lines is 0, since such lines either coincide or are parallel.

To determine the value of the angle between crossing straight lines, it is necessary to move both straight lines (or one of them) to a new position using the parallel transfer method before crossing. After that, you should find the value of the angle between the resulting intersecting straight lines.

You will need

Ruler, right triangle, pencil, protractor.

Instructions

So, let the vector V \u003d (a, b, c) and the plane A x + B y + C z \u003d 0 be given, where A, B and C are the coordinates of the normal N. Then the cosine of the angle α between vectors V and N is equal to: сos α \u003d (a A + b B + c C) / (√ (a² + b² + c²) √ (A² + B² + C²)).

To calculate the value of the angle in degrees or radians, you need to calculate the function inverse to the cosine from the resulting expression, i.e. arccosine: α \u003d arccos ((a A + b B + c C) / (√ (a² + b² + c²) √ (A² + B² + C²))).

Example: find angle between vector (5, -3, 8) and planegiven by the general equation 2 x - 5 y + 3 z \u003d 0 Solution: write down the coordinates of the normal vector of the plane N \u003d (2, -5, 3). Substitute all known values \u200b\u200binto the above formula: cos α \u003d (10 + 15 + 24) / √3724 ≈ 0.8 → α \u003d 36.87 °.

How to find an acute angle between straight lines. Angle between straight lines on a plane

The relative position of two straight lines

How to determine the relative position of two straight lines?

How to build a straight line parallel to a given one?

How to find the intersection point of two lines?

Perpendicular straight lines. Distance from point to line.Angle between straight lines

How to build a line perpendicular to a given one?

Distance from point to line

How to find the distance between two parallel lines?

Angle between two straight lines

Perpendicular straight lines. Distance from point to line.
Angle between straight lines