The video course "Get an A" includes all the topics necessary to successfully pass the exam in mathematics at 60-65 points. Completely all tasks 1-13 of the Profile Unified State Exam in Mathematics. Also suitable for passing the Basic exam in mathematics. If you want to pass the exam for 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!
Preparation course for the exam for grades 10-11, as well as for teachers. Everything you need to solve part 1 of the exam in mathematics (first 12 problems) and problem 13 (trigonometry). And this is more than 70 points on the exam, and neither a hundred-point student nor a humanities student can do without them.
All the theory you need. Fast ways solutions, traps and secrets of the exam. Disassembled all the relevant tasks of part 1 from the Bank of tasks of the FIPI. The course fully meets the requirements of the exam-2018.
The course contains 5 large topics, 2.5 hours each. Each topic is given from scratch, simple and straightforward.
Hundreds of exam assignments. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of exam assignments. Stereometry. Tricky solutions, helpful cheat sheets, developing spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Visual explanation of complex concepts. Algebra. Roots, degrees and logarithms, function and derivative. The basis for solving complex problems of the 2nd part of the exam.
A parallelogram is a quadrilateral in which opposite sides are pairwise parallel.
A parallelogram has all the properties of quadrangles, but besides that it has its own distinctive features... Knowing them, we can easily find both sides and angles of a parallelogram.
Parallelogram properties
- The sum of the angles in any parallelogram, as in any quadrilateral, is 360 °.
- The middle lines of a parallelogram and its diagonals intersect at one point and are divided by it in half. This point is usually called the center of symmetry of the parallelogram.
- Opposite sides of a parallelogram are always equal.
- Also, this figure always has opposite angles.
- The sum of the angles that adjoin either side of the parallelogram is always 180 °.
- The sum of the squares of the diagonals of a parallelogram is equal to twice the sum of the squares of its two adjacent sides. This is expressed by the formula:
- d 1 2 + d 2 2 = 2 (a 2 + b 2), where d 1 and d 2 are diagonals, a and b are adjacent sides.
- The cosine of an obtuse angle is always less than zero.
How to find the angles of a given parallelogram, applying these properties in practice? And what other formulas can help us with this? Consider the specific tasks that require: find the values of the angles of the parallelogram.
Finding the angles of a parallelogram
Case 1. The measure of an obtuse angle is known; it is required to find an acute angle.
Example: In parallelogram ABCD, angle A is 120 °. Find the measure of the remaining angles.
Solution: Using property 5, we can find the measure of the angle B adjacent to the angle given in the task. It will be equal to:
- 180 ° -120 ° = 60 °
Now, using property # 4, we determine that the two remaining angles C and D are opposite to the angles we have already found. Angle C is opposite to angle A, angle D is opposite to angle B. Therefore, they are equal to them in pairs.
- Answer: B = 60 °, C = 120 °, D = 60 °
Case 2. The lengths of the sides and diagonals are known
In this case, we need to use the cosine theorem.
We can first calculate the cosine of the angle we need using the formula, and then use a special table to find what the angle itself is.
For an acute angle, the formula is: 
- cosa = (A² + B² - d²) / (2 * A * B), where
- a is the required acute angle,
- A and B - sides of the parallelogram,
- d - smaller diagonal
For an obtuse angle, the formula changes slightly:
- cosß = (A² + B² - D²) / (2 * A * B), where
- ß is an obtuse angle,
- A and B - sides,
- D - large diagonal
Example: you need to find the acute angle of a parallelogram, the sides of which are 6 cm and 3 cm, and the smaller diagonal is 5.2 cm
Substitute the values into the formula for finding the acute angle:
- cosa = (6 2 + 3 2 - 5.2 2) / (2 * 6 * 3) = (36 + 9 - 27.04) / (2 * 18) = 17.96 / 36 ~ 18/36 ~ 1/2
- cosa = 1/2. According to the table, we find out that the desired angle is 60 °.
Problem 1... One of the angles of the parallelogram is 65 °. Find the rest of the angles of the parallelogram.
∠C = ∠A = 65 ° as opposite angles of the parallelogram.
∠А + ∠В = 180 ° as angles adjacent to one side of a parallelogram.
∠В = 180 ° - ∠А = 180 ° - 65 ° = 115 °.
∠D = ∠B = 115 ° as opposite angles of a parallelogram.
Answer: ∠А = ∠С = 65 °; ∠В = ∠D = 115 °.
Objective 2. The sum of the two angles of a parallelogram is 220 °. Find the angles of a parallelogram.
 Since the parallelogram has 2 equal sharp corners and 2 equal obtuse angles, then we are given the sum of two obtuse angles, i.e. ∠В + ∠D = 220 °. Then ∠В = ∠D = 220 ° :
2 = 110 °.
Since the parallelogram has 2 equal sharp corners and 2 equal obtuse angles, then we are given the sum of two obtuse angles, i.e. ∠В + ∠D = 220 °. Then ∠В = ∠D = 220 ° :
2 = 110 °.
∠А + ∠В = 180 ° as angles adjacent to one side of the parallelogram, therefore ∠А = 180 ° - ∠В = 180 ° - 110 ° = 70 °. Then ∠C = ∠A = 70 °.
Answer: ∠А = ∠С = 70 °; ∠В = ∠D = 110 °.
Objective 3. One of the corners of the parallelogram is 3 times larger than the other. Find the angles of a parallelogram.
Let ∠A = x. Then ∠B = 3x. Knowing that the sum of the angles of a parallelogram adjacent to one side of it is 180 °, we will compose an equation.
x = 180 : 4;
We get: ∠A = x = 45 °, and ∠B = 3x = 3 ∙ 45 ° = 135 °.
The opposite angles of the parallelogram are equal, therefore,
∠А = ∠С = 45 °; ∠В = ∠D = 135 °.
Answer: ∠А = ∠С = 45 °; ∠В = ∠D = 135 °.
Task 4. Prove that if a quadrangle has two sides parallel and equal, then this quadrilateral is a parallelogram.
Proof.
Let's draw a diagonal BD and consider Δ ADB and Δ CBD.
AD = BC by condition. The BD side is common. ∠1 = ∠2 as internal criss-crossing lines with parallel (by condition) lines AD and BC and secant line BD. Therefore, Δ ADB = Δ CBD on two sides and the angle between them (1st sign of equality of triangles). In equal triangles, the corresponding angles are equal, which means that ∠3 = ∠4. And these angles are internal crosswise at straight lines AB and CD and secant BD. This implies the parallelism of lines AB and CD. Thus, in a given quadrilateral ABCD, the opposite sides are pairwise parallel, therefore, by definition, ABCD is a parallelogram, which is what we had to prove.
Task 5. The two sides of a parallelogram are related as 2 : 5, and the perimeter is 3.5 m. Find the sides of the parallelogram.

∙ (AB + AD).
Let's denote one part by x. then AB = 2x, AD = 5x meters. Knowing that the perimeter of the parallelogram is 3.5 m, we compose the equation:
2 ∙ (2x + 5x) = 3.5;
2 ∙ 7x = 3.5;
x = 3.5 : 14;
One part is 0.25 m.Then AB = 2 ∙ 0.25 = 0.5 m; AD = 5 ∙ 0.25 = 1.25 m.
Examination.
Parallelogram perimeter P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1.75 = 3.5 (m).
Since the opposite sides of the parallelogram are equal, then CD = AB = 0.25 m; BC = AD = 1.25 m.
Answer: CD = AB = 0.25 m; BC = AD = 1.25 m.
A parallelogram is a quadrilateral in which the opposite sides are parallel, i.e. lie on parallel lines
Parallelogram properties: 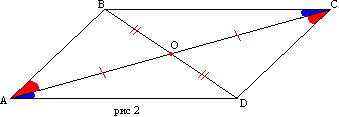 Theorem 22.
Opposite sides of a parallelogram are equal.
Theorem 22.
Opposite sides of a parallelogram are equal.
Proof. Draw a diagonal AC in the parallelogram ABCD. Triangles ACD and ACB are equal, as having a common side AC and two pairs of equal angles. adjacent to it: ∠ САВ = ∠ АСD, ∠ АСВ = ∠ DAC (as cross-lying angles with parallel lines AD and BC). Hence, AB = CD and BC = AD, as the corresponding sides of equal triangles, etc. The equality of these triangles also implies the equality of the corresponding angles of the triangles:
Theorem 23.
The opposite angles of the parallelogram are: ∠ A = ∠ C and ∠ B = ∠ D.
The equality of the first pair comes from the equality of triangles ABD and CBD, and the second - ABC and ACD.
Theorem 24.
Adjacent angles of the parallelogram, i.e. the angles adjacent to one side add up to 180 degrees.
This is because they are internal one-sided corners.
Theorem 25.
The diagonals of a parallelogram bisect each other at their intersection.
Proof. Consider triangles BOC and AOD. According to the first property, AD = BC ∠ OAD = ∠ OCB and ∠ ODA = ∠ OBC as criss-crossing at parallel lines AD and BC. Therefore, the triangles BOC and AOD are equal along the side and the corners adjacent to it. Hence, BO = OD and AO = OS, as the corresponding sides of equal triangles, etc.
Parallelogram signs
Theorem 26.
If the opposite sides of a quadrilateral are pairwise equal, then it is a parallelogram.
Proof. Let the quadrangle ABCD have the sides AD and BC, AB and CD, respectively (Fig. 2). Let's draw a diagonal AC. Triangles ABC and ACD are equal on three sides. Then the angles BAC and DCA are equal and, therefore, AB is parallel to CD. The parallelism of the sides BC and AD follows from the equality of the angles CAD and ACB.
Theorem 27.
If the opposite angles of a quadrilateral are pairwise equal, then it is a parallelogram.
Let ∠ A = ∠ C and ∠ B = ∠ D. Since ∠ А + ∠ В + ∠ С + ∠ D = 360 о, then ∠ А + ∠ В = 180 о and the sides AD and BC are parallel (on the basis of parallelism of straight lines). We will also prove the parallelism of the sides AB and CD and conclude that ABCD is a parallelogram by definition.
Theorem 28.
If the adjacent corners of the quadrilateral, i.e. angles adjacent to one side add up to 180 degrees, then it is a parallelogram.
If the inner one-sided angles add up to 180 degrees, then the straight lines are parallel. This means AB is parallel to CD and BC is parallel to AD. A quadrilateral turns out to be a parallelogram by definition.
Theorem 29.
If the diagonals of the quadrilateral are mutually divided at the point of intersection in half, then the quadrilateral is a parallelogram.
Proof. If AO = OC, BO = OD, then the triangles AOD and BOC are equal, as they have equal angles (vertical) at the vertex O, enclosed between pairs of equal sides. From the equality of the triangles, we conclude that AD and BC are equal. The sides AB and CD are also equal, and the quadrilateral turns out to be a parallelogram according to feature 1.
Theorem 30.
If a quadrilateral has a pair of equal, parallel sides, then it is a parallelogram.
Let the sides AB and CD be parallel and equal in the quadrangle ABCD. Let's draw the diagonals AC and BD. The parallelism of these straight lines implies the equality of the cross lying angles ABO = CDO and BAO = OCD. Triangles ABO and CDO are equal on the side and the angles adjacent to it. Therefore, AO = OC, BO = OD, i.e. the diagonals are halved by the intersection point and the quadrilateral turns out to be a parallelogram according to feature 4.
In geometry, special cases of a parallelogram are considered.
FOUR CORNERS.
§43. PARALLELOGRAM.
1. Definition of a parallelogram.
If we intersect a pair of parallel lines with another pair of parallel lines, then we get a quadrilateral, in which the opposite sides are pairwise parallel.
In the quadrangles ABDC and EFNM (drawing 224) BD || AC and AB || CD;
ЕF || МN and ЕМ || FN.
A quadrilateral whose opposite sides are pairwise parallel is called a parallelogram.
2. Properties of the parallelogram.
Theorem. The diagonal of the parallelogram divides it into two equal triangles.
Let there be a parallelogram ABDC (Fig. 225), in which AB || CD and AC || BD.
It is required to prove that the diagonal divides it into two equal triangles.
Let's draw the diagonal CB in the parallelogram ABDC. Let us prove that /\ CAB = /\ CDB.
The CB side is common for these triangles; / ABC = / ВСD, as internal criss-crossing angles with parallel AB and CD and secant CB; / ASV = / CBD, also as internal cross-lying angles with parallel AC and BD and secant CB (§ 38).

From here /\ CAB = /\ CDB.
In the same way, one can prove that the diagonal AD will divide the parallelogram into two equal triangles ACD and ABD.
Consequences. 1 . Opposite angles of a parallelogram are equal to each other.
/
A = /
D, this follows from the equality of triangles CAB and CDB.
Likewise /
C = /
V.
2. Opposite sides of a parallelogram are equal to each other.
AB = CD and AC = BD, since these are the sides of equal triangles and lie opposite equal angles.
Theorem 2. The diagonals of the parallelogram are halved at the point of their intersection.
Let BC and AD be the diagonals of the parallelogram ABDC (Fig. 226). Let us prove that AO = OD and CO = OB.
To do this, compare any pair of opposite triangles, for example /\ AOB and /\ COD.
In these triangles AB = CD, as opposite sides of a parallelogram;
/
1 = /
2, as the internal angles in a cross lying with parallel AB and CD and secant AD;
/
3 = /
4 for the same reason, since AB || CD and CB are their secant (§ 38).
Hence it follows that /\ AОВ = /\ COD. And in equal triangles opposite equal angles there are equal sides. Therefore, AO = OD and CO = OB.
Theorem 3. The sum of the angles adjacent to one side of the parallelogram is 2 d .
Prove yourself.
3. Signs of a parallelogram.
Theorem. If the opposite sides of the quadrilateral are pairwise equal, then this quadrilateral is a parallelogram.
Let in the quadrilateral ABDC (Fig. 227) AB = CD and AC = BD. Let us prove that under this condition AB || CD and AC || ВD, i.e. the quadrilateral ABDC is a parallelogram.
Let's connect by a segment any two opposite vertices of this - a quadrilateral, for example, C and B. Quadrilateral ABDC split into two equal triangles: /\
CAB and /\
CDB. In fact, they have a common side CB, AB = CD and AC = BD by condition. Thus, the three sides of one triangle are respectively equal to the three sides of the other, therefore /\
CAB = /\
CDB.

In equal triangles against equal sides lie equal angles, therefore
/
1 = /
2 and /
3 = /
4.
Angles 1 and 2 are internal criss-crossing angles at the intersection of straight lines AB and CD of straight line CB. Therefore, AB || CD.
In the same way, the 3rd and 4th angles are internal criss-crossing angles at the intersection of lines CA and BD of straight line CB, therefore, CA || BD (§ 35).
Thus, the opposite sides of the quadrilateral ABDC are pairwise parallel, therefore, it is a parallelogram, which is what was required to be proved.
Theorem 2. If two opposite sides of a quadrilateral are equal and parallel, then this quadrilateral is a parallelogram.
Let in the quadrilateral ABDС AB = CD and AB || CD. Let us prove that under these conditions the quadrilateral ABDC is a parallelogram (Fig. 228).

Let us connect the vertices C and B with a segment CB. Due to the parallelism of lines AB and CD, angles 1 and 2, as internal angles lying in a cross, are equal (§ 38).
Then the triangle CAB equal to triangle CDB, since they have a common CB side,
AB = CD by the condition of the theorem and /
1 = /
2 as proved. The equality of these triangles implies the equality of angles 3 and 4, since they lie opposite equal sides in equal triangles.
But angles 3 and 4 are internal cross-lying angles formed at the intersection of straight lines AC and BD of straight line CB, therefore, AC || BD (§ 35), i.e. the quadrilateral
ABDC - parallelogram.
Exercises.
1. Prove that if the diagonals of a quadrilateral at the point of their mutual intersection are halved, then this quadrilateral is a parallelogram.
2. Prove that a quadrilateral whose sum inner corners adjacent to each of two adjacent sides is equal to 2 d, there is a parallelogram.
3. Construct a parallelogram along two sides and an angle between them:
a) using the parallelism of the opposite sides of the parallelogram;
b) using the equality of opposite sides of the parallelogram.
4. Construct a parallelogram along two adjacent sides and a diagonal.
5. Construct a parallelogram along its two diagonals and the angle between them.
6. Construct a parallelogram along its side and two diagonals.
