A „Get A” videótanfolyam tartalmazza az összes olyan témát, amely a matematika egységes államvizsga sikeres letételéhez szükséges 60-65 ponttal. Teljesen a Profil egységes államvizsga matematika 1-13. Matematika egységes államvizsga alapvizsga letételére is alkalmas. Ha 90-100 ponttal szeretnél letenni az egységes államvizsgát, akkor az 1. részt 30 perc alatt és hiba nélkül kell megoldanod!
Egységes államvizsgára felkészítő tanfolyam 10-11. évfolyam, valamint pedagógusok számára. Minden, ami az egységes államvizsga 1. részének matematikából (az első 12 feladat) és a 13. feladat (trigonometria) megoldásához szükséges. Ez pedig több mint 70 pont az egységes államvizsgán, és ezek nélkül sem egy 100 pontos, sem egy bölcsész nem megy.
Minden szükséges elmélet. Gyors módszerek az egységes államvizsga megoldásai, buktatói és titkai. A FIPI Feladatbank 1. részének minden aktuális feladatát elemezték. A tanfolyam teljes mértékben megfelel az Egységes Államvizsga 2018 követelményeinek.
A tanfolyam 5 nagy témát tartalmaz, egyenként 2,5 órás. Minden témát a semmiből adunk, egyszerűen és világosan.
Több száz egységes államvizsga-feladat. Szöveges feladatok és valószínűségszámítás. Egyszerű és könnyen megjegyezhető algoritmusok a problémák megoldására. Geometria. Elmélet, referencia anyag, minden típusú egységes államvizsga-feladat elemzése. Sztereometria. Trükkös megoldások, hasznos csalólapok, térbeli fantázia fejlesztése. Trigonometria a semmiből a feladatig 13. Megértés a zsúfoltság helyett. Komplex fogalmak világos magyarázata. Algebra. Gyökök, hatványok és logaritmusok, függvény és derivált. Az egységes államvizsga 2. részében szereplő összetett problémák megoldásának alapja.
A paralelogramma olyan négyszög, amelyben a szemközti oldalak páronként párhuzamosak.
A paralelogramma rendelkezik a négyszögek összes tulajdonságával, de emellett megvan a sajátja is megkülönböztető jellegzetességek. Ezek ismeretében könnyen megtalálhatjuk a paralelogramma oldalait és szögeit is.
A paralelogramma tulajdonságai
- A szögek összege bármely paralelogrammában, akárcsak minden négyszögben, 360°.
- A paralelogramma középvonalai és átlói egy pontban metszik egymást, és ez kettévágja őket. Ezt a pontot szokás a paralelogramma szimmetriaközéppontjának nevezni.
- A paralelogramma szemközti oldalai mindig egyenlőek.
- Ezenkívül ennek az alaknak mindig egyenlő ellentétes szögei vannak.
- A paralelogramma bármelyik oldalával szomszédos szögek összege mindig 180°.
- Egy paralelogramma átlóinak négyzetösszege egyenlő a két szomszédos oldala négyzetösszegének kétszeresével. Ezt a következő képlet fejezi ki:
- d 1 2 + d 2 2 = 2 (a 2 + b 2), ahol d 1 és d 2 átlók, a és b szomszédos oldalak.
- A tompaszög koszinusza mindig kisebb, mint nulla.
Hogyan találjuk meg egy adott paralelogramma szögeit ezen tulajdonságok felhasználásával a gyakorlatban? És milyen egyéb képletek segíthetnek ebben? Nézzük meg a konkrét feladatokat, amelyekhez szükség van: keressük meg a paralelogramma szögeit.
A paralelogramma szögeinek megkeresése
1. eset. A tompaszög mértéke ismert, meg kell találnunk a hegyesszöget.
Példa: Az ABCD paralelogrammában az A szög 120°. Keresse meg a fennmaradó szögek mértékét.
Megoldás: Az 5. számú tulajdonság segítségével megtalálhatjuk a feladatban megadott szög melletti B szög mértékét. Ez egyenlő lesz:
- 180°-120° = 60°
És most a 4-es tulajdonság felhasználásával meghatározzuk, hogy a két fennmaradó C és D szög ellentétes a már talált szögekkel. A C szög ellentétes az A szöggel, a D szög ellentétes a B szöggel. Ezért páronként egyenlőek.
- Válasz: B = 60°, C = 120°, D = 60°
2. eset. Az oldalak és az átlók hossza ismert
Ebben az esetben a koszinusz tételt kell használnunk.
Először a képlet segítségével kiszámíthatjuk a szükséges szög koszinuszát, majd egy speciális táblázat segítségével megkereshetjük, hogy maga a szög mekkora szöggel egyenlő.
Hegyesszög esetén a képlet a következő: 
- cosa = (A² + B² - d²) / (2 * A * B), ahol
- a a kívánt hegyesszög,
- A és B a paralelogramma oldalai,
- d - kisebb átló
Tompaszög esetén a képlet kissé megváltozik:
- cosß = (A² + B² - D²) / (2 * A * B), ahol
- ß tompaszög,
- A és B oldalak
- D - nagy átlós
Példa: meg kell találnia a paralelogramma hegyesszögét, amelynek oldalai 6 cm és 3 cm, a kisebb átlója pedig 5,2 cm
Helyettesítse be az értékeket a képletbe, hogy hegyesszöget találjon:
- cosa = (6 2 + 3 2 - 5,2 2) / (2 * 6 * 3) = (36 + 9 - 27,04) / (2 * 18) = 17,96/36 ~ 18/36 ~ 1/2
- cosa = 1/2. A táblázatból kiderül, hogy a kívánt szög 60°.
1. probléma. A paralelogramma egyik szöge 65°. Keresse meg a paralelogramma fennmaradó szögeit!
∠C =∠A = 65°, mint egy paralelogramma szemközti szöge.
∠A +∠B = 180°, mint a paralelogramma egyik oldalával szomszédos szögek.
∠B = 180° - ∠A = 180° - 65° = 115°.
∠D =∠B = 115°, mint a paralelogramma szemközti szögei.
Válasz: ∠A =∠C = 65°; ∠B =∠D = 115°.
2. feladat. Egy paralelogramma két szögének összege 220°. Keresse meg a paralelogramma szögeit!
 Mivel egy paralelogrammának 2 egyenlő hegyesszögekés 2 egyenlő tompaszög, akkor megadjuk két tompaszög összegét, azaz. ∠B +∠D = 220°. Ekkor ∠B =∠D = 220° :
2 = 110°.
Mivel egy paralelogrammának 2 egyenlő hegyesszögekés 2 egyenlő tompaszög, akkor megadjuk két tompaszög összegét, azaz. ∠B +∠D = 220°. Ekkor ∠B =∠D = 220° :
2 = 110°.
∠A + ∠B = 180°, mint a paralelogramma egyik oldalával szomszédos szögek, tehát ∠A = 180° - ∠B = 180° - 110° = 70°. Ekkor ∠C =∠A = 70°.
Válasz: ∠A =∠C = 70°; ∠B =∠D = 110°.
3. feladat. A paralelogramma egyik szöge háromszor nagyobb, mint a másik. Keresse meg a paralelogramma szögeit!
Legyen ∠A =x. Ekkor ∠B = 3x. Tudva, hogy az egyik oldalával szomszédos paralelogramma szögeinek összege 180°, egy egyenletet készítünk.
x = 180 : 4;
A következőt kapjuk: ∠A = x = 45°, és ∠B = 3x = 3 ∙ 45° = 135°.
A paralelogramma ellentétes szögei egyenlőek, ezért
∠A =∠C = 45°; ∠B =∠D = 135°.
Válasz: ∠A =∠C = 45°; ∠B =∠D = 135°.
4. feladat. Bizonyítsuk be, hogy ha egy négyszögnek két párhuzamos és egyenlő oldala van, akkor ez a négyszög paralelogramma.
Bizonyíték.
Rajzoljuk meg a BD átlót, és vegyük figyelembe Δ ADB és Δ CBD.
AD = Kr. e. feltétel szerint. A BD oldal gyakori. ∠1 = ∠2 belső keresztben fekvő párhuzamos (feltétel szerint) AD és BC egyenesekkel és BD metszővel. Ezért Δ ADB = Δ CBD két oldalon és a köztük lévő szög (a háromszögek egyenlőségének 1. jele). Egybevágó háromszögekben a megfelelő szögek egyenlőek, ami azt jelenti, hogy ∠3 =∠4. És ezek a szögek olyan belső szögek, amelyek keresztben fekszenek az AB és CD egyenesekkel és a BD metszővel. Ez azt jelenti, hogy az AB és a CD egyenesek párhuzamosak. Ebben az ABCD négyszögben tehát a szemközti oldalak páronként párhuzamosak, ezért definíció szerint az ABCD paralelogramma, amit bizonyítani kellett.
5. feladat. A paralelogramma két oldalának aránya 2 : 5, kerülete pedig 3,5 m. Keresse meg a paralelogramma oldalait.

∙ (AB + AD).
Jelöljük az egyik részt x-szel. akkor AB = 2x, AD = 5x méter. Tudva, hogy a paralelogramma kerülete 3,5 m, létrehozzuk az egyenletet:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
x = 3,5 : 14;
Egy rész 0,25 m Ekkor AB = 2 ∙ 0,25 = 0,5 m; AD = 5 ∙ 0,25 = 1,25 m.
Vizsgálat.
A P ABCD paralelogramma kerülete = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (m).
Mivel a paralelogramma szemközti oldalai egyenlőek, akkor CD = AB = 0,25 m; BC = Kr. = 1,25 m.
Válasz: CD = AB = 0,25 m; BC = Kr. = 1,25 m.
A paralelogramma olyan négyszög, amelynek szemközti oldalai párhuzamosak, azaz. párhuzamos egyeneseken feküdjön
A paralelogramma tulajdonságai: 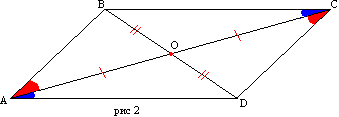 22. tétel.
A paralelogramma szemközti oldalai egyenlőek.
22. tétel.
A paralelogramma szemközti oldalai egyenlőek.
Bizonyíték. Az ABCD paralelogrammában AC átlót rajzolunk. Az ACD és az ACB háromszögek egybevágóak, mivel közös AC oldaluk és két egyenlő szögpárjuk van. mellette: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (mint keresztirányú szögek AD és BC párhuzamos egyenesekkel). Ez azt jelenti, hogy AB = CD és BC = AD, mint egyenlő háromszögek megfelelő oldalai stb. E háromszögek egyenlőségéből az is következik, hogy a háromszögek megfelelő szögei egyenlőek:
23. tétel.
A paralelogramma szemközti szögei egyenlőek: ∠ A=∠ C és ∠ B=∠ D.
Az első pár egyenlősége az ABD és a CBD háromszögek egyenlőségéből származik, a második pedig az ABC és az ACD háromszögek egyenlőségéből.
24. tétel.
Egy paralelogramma szomszédos szögei, azaz. az egyik oldallal szomszédos szögek 180 fokot adnak össze.
Ez azért van így, mert belső egyoldalú szögek.
25. tétel.
A paralelogramma átlói metszéspontjukban felezik egymást.
Bizonyíték. Tekintsük a BOC és AOD háromszögeket. Az első tulajdonság szerint AD=BC ∠ OAD=∠ OCB és ∠ ODA=∠ OBC keresztben fekvő AD és BC párhuzamos egyenesekre. Ezért a BOC és AOD háromszög oldal- és szomszédos szöge egyenlő. Ez azt jelenti, hogy BO=OD és AO=OS, mint az egyenlő háromszögek megfelelő oldalai stb.
A paralelogramma jelei
26. tétel.
Ha egy négyszög szemközti oldalai páronként egyenlőek, akkor ez paralelogramma.
Bizonyíték. Legyen az ABCD négyszög AD és BC, AB és CD oldala rendre egyenlő (2. ábra). Rajzoljuk meg az AC átlót. Az ABC és az ACD háromszög három oldala egyenlő. Ekkor a BAC és a DCA szögek egyenlőek, és ezért AB párhuzamos CD-vel. A BC és AD oldalak párhuzamossága a CAD és ACB szögek egyenlőségéből következik.
27. tétel.
Ha egy négyszög szemközti szögei páronként egyenlőek, akkor ez paralelogramma.
Legyen ∠ A=∠ C és ∠ B=∠ D. Mert ∠ A+∠ B+∠ C+∠ D=360 o, majd ∠ A+∠ B=180 o és AD és BC oldalak párhuzamosak (az egyenesek párhuzamossága alapján). Az AB és CD oldalak párhuzamosságát is bizonyítjuk, és arra a következtetésre jutunk, hogy az ABCD definíció szerint paralelogramma.
28. tétel.
Ha egy négyszög szomszédos sarkai, pl. Az egyik oldallal szomszédos szögek 180 fokot adnak össze, akkor ez egy paralelogramma.
Ha a belső egyoldali szögek 180 fokot adnak össze, akkor az egyenesek párhuzamosak. Tehát AB párhuzamos CD-vel és BC párhuzamos AD-vel. A négyszög definíció szerint paralelogramma.
29. tétel.
Ha egy négyszög átlói a metszéspontban felezik egymást, akkor a négyszög paralelogramma.
Bizonyíték. Ha AO = OC, BO = OD, akkor az AOD és a BOC háromszögek egyenlőek, mivel egyenlő (függőleges) szögeik vannak az O csúcsban, és egyenlő oldalpárok közé záródnak. A háromszögek egyenlőségéből azt a következtetést vonjuk le, hogy AD és BC egyenlők. Az AB és a CD oldalak is egyenlőek, és a négyszög az 1. kritérium szerint paralelogrammának bizonyul.
30. tétel.
Ha egy négyszögnek van egy pár egyenlő, párhuzamos oldala, akkor paralelogramma.
Legyenek az ABCD négyszög AB és CD oldalai párhuzamosak és egyenlők. Rajzoljunk AC és BD átlókat. Ezen egyenesek párhuzamosságából az következik, hogy az ABO = CDO és BAO = OCD keresztirányú szögek egyenlőek. Az ABO és CDO háromszögek oldal- és szomszédos szögei egyenlőek. Ezért AO=OS, VO=ОD, azaz. Az átlókat kettéosztja a metszéspont, és a négyszög a 4. kritérium szerint paralelogrammának bizonyul.
A geometriában a paralelogrammák speciális eseteit veszik figyelembe.
QUADAGONS.
43. §. PARALELOGRAMMA.
1. A paralelogramma definíciója.
Ha egy pár párhuzamos egyenest metszünk egy másik pár párhuzamos egyenessel, akkor olyan négyszöget kapunk, amelynek szemközti oldalai páronként párhuzamosak.
Az ABC és EFNM négyszögekben (224. ábra) ВD || AC és AB || CD;
EF || MN és EM || FN.
Azt a négyszöget, amelynek szemközti oldalai páronként párhuzamosak, paralelogrammának nevezzük.
2. A paralelogramma tulajdonságai.
Tétel. A paralelogramma átlója két egyenlő háromszögre osztja.
Legyen egy ABC paralelogramma (225. ábra), amelyben AB || CD és AC || ВD.
Be kell bizonyítani, hogy az átló két egyenlő háromszögre osztja.
Rajzoljunk CB átlót az ABC paralelogrammába. Bizonyítsuk be /\ CAB= /\ C.D.B.
Az ÉK oldal közös ezekben a háromszögekben; / ABC = / BCD, mint belső keresztirányú szögek párhuzamos AB-vel és CD-vel, valamint a CB szekánssal; / DIA = / СВD, mint a belső keresztirányú szögek párhuzamos AC és ВD és szekáns CB mellett (38. §).

Innen /\ CAB = /\ C.D.B.
Ugyanígy bebizonyítható, hogy az AD átló a paralelogrammát két egyenlő ACD és ABD háromszögre osztja.
Következmények. 1 . A paralelogramma ellentétes szögei egyenlőek egymással.
/
A = /
D, ez a CAB és CDB háromszögek egyenlőségéből következik.
Hasonlóképpen /
C = /
BAN BEN.
2. A paralelogramma szemközti oldalai egyenlőek egymással.
AB = CD és AC = BD, mivel ezek egyenlő háromszögek oldalai és egyenlő szögekkel ellentétesek.
2. tétel. A paralelogramma átlóit a metszéspontjukban kettéosztjuk.
Legyen BC és AD az ABC paralelogramma átlói (226. ábra). Bizonyítsuk be, hogy AO = OD és CO = OB.
Ehhez hasonlítson össze például néhány szemközti háromszögpárt /\ AOB és /\ TŐKEHAL.
Ezekben a háromszögekben AB = CD, mint egy paralelogramma szemközti oldalai;
/
1 = /
2, mint az AB és a CD párhuzamossal keresztbe eső belső szögek és AD szekáns;
/
3 = /
4 ugyanezen okból, mivel az AB || CD és CB a szekánsuk (38. §).
Ebből következik, hogy /\ AOB = /\ TŐKEHAL. És egyenlő háromszögekben az egyenlő oldalak egyenlő szögekkel ellentétesek. Ezért AO = OD és CO = OB.
3. tétel. A paralelogramma egyik oldalával szomszédos szögek összege egyenlő 2 d .
Bizonyítsd be magad.
3. A paralelogramma jelei.
Tétel. Ha egy négyszög szemközti oldalai páronként egyenlőek, akkor ez a négyszög paralelogramma.
Legyen az ABC négyszögben (227. rajz) AB = CD és AC = BD. Bizonyítsuk be, hogy ezen feltétel mellett AB || CD és AC || A ВD, azaz a АВDC négyszög egy paralelogramma.
Kössünk egy szakaszhoz ennek a négyszögnek két ellentétes csúcsát, például C-t és B-t. Az ABCD négyszöget két egyenlő háromszögre osztjuk: /\
CAB és /\
СДВ. Valójában ugyanaz a CB oldaluk, AB = CD és AC = BD a feltételnek megfelelően. Tehát egy háromszög három oldala rendre egyenlő egy másik háromszög három oldalával /\
CAB = /\
C.D.B.

Az egyenlő háromszögekben egyenlő oldalak vannak egymással szemben egyenlő szögek, Ezért
/
1 = /
2 és /
3 = /
4.
Az 1 és 2 szögek a CB egyenes AB és CD metszéspontjában keresztben elhelyezkedő belső szögek. Ezért AB || CD.
Ugyanígy a 3. és 4. szög a CB egyenes CA és BD vonalainak metszéspontjában keresztben elhelyezkedő belső szögek, ezért CA || ВD (35. §).
Így az ABCD négyszög szemközti oldalai páronként párhuzamosak, tehát paralelogramma, amit bizonyítani kellett.
2. tétel. Ha egy négyszög két szemközti oldala egyenlő és párhuzamos, akkor a négyszög paralelogramma.
Legyen AB = CD az ABCD négyszögben és AB || CD. Bizonyítsuk be, hogy ilyen feltételek mellett az ABC négyszög paralelogramma (228. ábra).

Kössük össze a C és B csúcsokat egy CB szakaszlal Az AB és CD egyenesek párhuzamossága miatt az 1 és 2, mint keresztben fekvő belső szögek egyenlőek (38. §).
Ezután háromszög CAB egyenlő egy háromszöggel CDB, mivel ugyanaz az ÉK oldaluk,
AB = CD a tétel feltételei szerint és /
1 = /
2 szerint bevált. Ezeknek a háromszögeknek az egyenlősége magában foglalja a 3 és 4 szögek egyenlőségét, mivel egyenlő háromszögekben egymással szemben helyezkednek el.
De a 3 és 4 szögek belső keresztirányú szögek, amelyeket a CB egyenes AC és BD metszéspontja alkot, ezért AC || ВD (35. §), azaz négyszög
Az ABC egy paralelogramma.
Feladatok.
1. Bizonyítsuk be, hogy ha egy négyszög átlóit a metszéspontjukban kettéosztjuk, akkor ez a négyszög paralelogramma.
2. Bizonyítsuk be, hogy egy négyszög, amelynek összege belső sarkok a két szomszédos oldal mindegyike mellett egyenlő 2 d, van egy paralelogramma.
3. Szerkesszünk paralelogrammát két oldal és a köztük lévő szög felhasználásával:
a) egy paralelogramma szemközti oldalainak párhuzamosságának felhasználásával;
b) egy paralelogramma szemközti oldalainak egyenlőségét felhasználva.
4. Szerkesszünk paralelogrammát két szomszédos oldal és egy átló segítségével!
5. Szerkesszünk paralelogrammát a két átlója és a közöttük lévő szög felhasználásával!
6. Szerkesszünk paralelogrammát oldalának és két átlójának felhasználásával!
