Hvad er summen af ​​ensidede vinkler i et parallelogram? Parallelogram

Videokurset "Få et A" inkluderer alle de emner, der er nødvendige for at bestå Unified State Examen i matematik med 60-65 point. Fuldstændig alle opgave 1-13 i Profile Unified State eksamen i matematik. Også egnet til at bestå Basic Unified State Examination i matematik. Hvis du vil bestå Unified State-eksamenen med 90-100 point, skal du løse del 1 på 30 minutter og uden fejl!

Forberedelseskursus til Unified State Examen for klasse 10-11, samt for lærere. Alt hvad du behøver for at løse del 1 af Unified State-eksamenen i matematik (de første 12 opgaver) og opgave 13 (trigonometri). Og det er mere end 70 point på Unified State Exam, og hverken en 100-point studerende eller en humaniora-studerende kan undvære dem.

Al den nødvendige teori. Hurtige måder løsninger, faldgruber og hemmeligheder ved Unified State Exam. Alle aktuelle opgaver i del 1 fra FIPI Task Bank er blevet analyseret. Kurset overholder fuldt ud kravene i Unified State Exam 2018.

Kurset indeholder 5 store emner, 2,5 time hver. Hvert emne er givet fra bunden, enkelt og tydeligt.

Hundredvis af Unified State Exam-opgaver. Ordproblemer og sandsynlighedsteori. Enkle og nemme at huske algoritmer til løsning af problemer. Geometri. Teori, referencemateriale, analyse af alle typer Unified State Examination opgaver. Stereometri. Vanskelige løsninger, nyttige snydeark, udvikling af rumlig fantasi. Trigonometri fra bunden til opgave 13. Forståelse i stedet for at proppe. Klare forklaringer af komplekse begreber. Algebra. Rødder, potenser og logaritmer, funktion og afledet. Et grundlag for at løse komplekse problemer i del 2 af Unified State Exam.

Et parallelogram er en firkant, hvor modsatte sider er parallelle i par.

Et parallelogram har alle firkanters egenskaber, men derudover har det også sine egne særpræg. Når vi kender dem, kan vi nemt finde både siderne og vinklerne på et parallelogram.

Egenskaber for et parallelogram

1. Summen af ​​vinklerne i ethvert parallelogram, som i enhver firkant, er 360°.
2. Midtlinjerne i et parallelogram og dets diagonaler skærer hinanden i et punkt og er halveret af det. Dette punkt kaldes normalt parallelogrammets symmetricenter.
3. De modsatte sider af et parallelogram er altid lige store.
4. Også denne figur har altid lige modsatte vinkler.
5. Summen af ​​vinklerne, der støder op til en af ​​siderne af et parallelogram, er altid 180°.
6. Summen af ​​kvadraterne af diagonalerne i et parallelogram er lig med to gange summen af ​​kvadraterne på dets to tilstødende sider. Dette er udtrykt ved formlen:
   • d 1 2 + d 2 2 = 2 (a 2 + b 2), hvor d 1 og d 2 er diagonaler, a og b er tilstødende sider.
7. Cosinus for en stump vinkel er altid mindre end nul.

Hvordan finder man vinklerne for et givet parallelogram ved hjælp af disse egenskaber i praksis? Og hvilke andre formler kan hjælpe os med dette? Lad os se på specifikke opgaver, der kræver: find vinklerne på et parallelogram.

Find vinklerne på et parallelogram

Case 1. Målingen af ​​en stump vinkel er kendt, vi skal finde en spids vinkel.

Eksempel: I parallelogram ABCD er vinkel A 120°. Find målet for de resterende vinkler.

Løsning: Ved hjælp af egenskab nr. 5 kan vi finde målet for vinklen B, der støder op til den vinkel, der er givet i opgaven. Det vil være lig med:

• 180°-120°= 60°

Og nu, ved hjælp af egenskab nr. 4, bestemmer vi, at de to resterende vinkler C og D er modsatte af de vinkler, som vi allerede har fundet. Vinkel C er modsat vinkel A, vinkel D er modsat vinkel B. Derfor er de parvis lige store.

• Svar: B = 60°, C = 120°, D=60°

Tilfælde 2. Længden af ​​siderne og diagonalerne er kendt

I dette tilfælde skal vi bruge cosinussætningen.

Vi kan først beregne cosinus for den vinkel, vi skal bruge, ved hjælp af en formel, og derefter bruge en speciel tabel til at finde, hvad selve vinklen er lig med.

For en spids vinkel er formlen:

• cosa = (A² + B² - d²) / (2 * A * B), hvor
• a er den ønskede spidse vinkel,
• A og B er siderne af parallelogrammet,
• d - mindre diagonal

For en stump vinkel ændres formlen lidt:

• cosß = (A² + B² - D²) / (2 * A * B), hvor
• ß er en stump vinkel,
• A og B er sider
• D - stor diagonal

Eksempel: du skal finde en spids vinkel på et parallelogram, hvis sider er 6 cm og 3 cm, og den mindre diagonal er 5,2 cm

Erstat værdierne i formlen for at finde en spids vinkel:

• cosa = (6 2 + 3 2 - 5,2 2) / (2 * 6 * 3) = (36 + 9 - 27,04) / (2 * 18) = 17,96/36 ~ 18/36 ~ 1/2
• cosa = 1/2. Fra tabellen finder vi ud af, at den ønskede vinkel er 60°.

Opgave 1. En af vinklerne i parallelogrammet er 65°. Find de resterende vinkler af parallelogrammet.

∠C =∠A = 65° som modsatte vinkler af et parallelogram.

∠A +∠B = 180° som vinkler, der støder op til den ene side af et parallelogram.

∠B = 180° - ∠A = 180° - 65° = 115°.

∠D =∠B = 115° som de modsatte vinkler af et parallelogram.

Svar: ∠A =∠C = 65°; ∠B =∠D = 115°.

Opgave 2. Summen af ​​to vinkler i et parallelogram er 220°. Find vinklerne på parallelogrammet.

Da et parallelogram har 2 ens spidse vinkler og 2 lige store stumpe vinkler, så får vi summen af ​​to stumpe vinkler, dvs. ∠B +∠D = 220°. Så ∠B =∠D = 220° : 2 = 110°.

∠A + ∠B = 180° som vinkler, der støder op til den ene side af et parallelogram, så ∠A = 180° - ∠B = 180° - 110° = 70°. Derefter ∠C =∠A = 70°.

Svar: ∠A =∠C = 70°; ∠B =∠D = 110°.

Opgave 3. En af vinklerne i et parallelogram er 3 gange større end den anden. Find vinklerne på parallelogrammet.

Lad ∠A =x. Så ∠B = 3x. Når vi ved, at summen af ​​vinklerne på et parallelogram, der støder op til en af ​​dets sider, er lig med 180°, vil vi lave en ligning.

x = 180 : 4;

Vi får: ∠A = x = 45°, og ∠B = 3x = 3 ∙ 45° = 135°.

Modsatte vinkler af et parallelogram er ens, derfor

∠A =∠C = 45°; ∠B =∠D = 135°.

Svar: ∠A =∠C = 45°; ∠B =∠D = 135°.

Opgave 4. Bevis, at hvis en firkant har to parallelle og lige sider, så er denne firkant et parallelogram.

Bevis.

Lad os tegne diagonalen BD og overveje Δ ADB og Δ CBD.

AD = BC efter betingelse. BD-siden er almindelig. ∠1 = ∠2 som indre tværgående liggende med parallelle (efter betingelse) linjer AD og BC og sekant BD. Derfor er Δ ADB = Δ CBD på to sider og vinklen mellem dem (1. tegn på trekanters lighed). I kongruente trekanter er de tilsvarende vinkler ens, hvilket betyder ∠3 =∠4. Og disse vinkler er indre vinkler, der ligger på tværs med rette linjer AB og CD og sekant BD. Dette indebærer, at linjerne AB og CD er parallelle. Således, i denne firkantede ABCD, er de modsatte sider parallelle i par, derfor er ABCD per definition et parallelogram, hvilket er det, der skulle bevises.

Opgave 5. De to sider af et parallelogram er i forholdet 2 : 5, og omkredsen er 3,5 m. Find siderne af parallelogrammet.

∙ (AB + AD).

Lad os betegne en del med x. så AB = 2x, AD = 5x meter. Ved at vide, at omkredsen af ​​parallelogrammet er 3,5 m, skaber vi ligningen:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

x = 3,5 : 14;

En del er 0,25 m. Så er AB = 2 ∙ 0,25 = 0,5 m; AD = 5 ∙ 0,25 = 1,25 m.

Undersøgelse.

Omkreds af parallelogram P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (m).

Da de modsatte sider af parallelogrammet er ens, så CD = AB = 0,25 m; BC = AD = 1,25 m.

Svar: CD = AB = 0,25 m; BC = AD = 1,25 m.

Et parallelogram er en firkant, hvis modsatte sider er parallelle, dvs. ligge på parallelle linjer

Egenskaber for et parallelogram: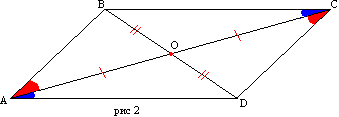
Sætning 22. Modsatte sider af et parallelogram er lige store.
Bevis. I parallelogrammet ABCD tegner vi en diagonal AC. Trekanter ACD og ACB er kongruente, idet de har en fælles side AC og to par lige store vinkler. ved siden af: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (som tværgående vinkler med parallelle linjer AD og BC). Det betyder, at AB = CD og BC = AD, som de tilsvarende sider af lige store trekanter osv. Af ligheden af ​​disse trekanter følger det også, at de tilsvarende vinkler i trekanter er ens:
Sætning 23. De modsatte vinkler af parallelogrammet er ens: ∠ A=∠ C og ∠ B=∠ D.
Ligheden af ​​det første par kommer fra ligheden af ​​trekanter ABD og CBD, og ​​det andet - ABC og ACD.
Sætning 24. Tilstødende vinkler af et parallelogram, dvs. vinkler, der støder op til den ene side, er op til 180 grader.
Dette er tilfældet, fordi de er indvendige ensidede vinkler.
Sætning 25. Diagonalerne i et parallelogram halverer hinanden ved deres skæringspunkt.
Bevis. Overvej trekanter BOC og AOD. Ifølge den første egenskab AD=BC ∠ OAD=∠ OCB og ∠ ODA=∠ OBC liggende på tværs for parallelle linjer AD og BC. Derfor er trekanter BOC og AOD ens i side- og tilstødende vinkler. Dette betyder BO=OD og AO=OS, ligesom de tilsvarende sider af lige store trekanter osv.

Tegn på et parallelogram
Sætning 26. Hvis de modsatte sider af en firkant er parvis lige store, så er det et parallelogram.
Bevis. Lad firkanten ABCD have siderne AD og BC, AB og CD henholdsvis lige store (fig. 2). Lad os tegne den diagonale AC. Trekanter ABC og ACD er lige store på tre sider. Så er vinklerne BAC og DCA ens, og derfor er AB parallel med CD. Parallellen mellem siderne BC og AD følger af ligheden mellem vinklerne CAD og ACB.
Sætning 27. Hvis de modsatte vinkler af en firkant er parvis lige store, så er det et parallelogram.
Lad ∠ A=∠ C og ∠ B=∠ D. Fordi ∠ A+∠ B+∠ C+∠ D=360 o, så ∠ A+∠ B=180 o og siderne AD og BC er parallelle (baseret på lige linjers parallellitet). Vi vil også bevise paralleliteten mellem siderne AB og CD og konkludere, at ABCD per definition er et parallelogram.
Sætning 28. Hvis tilstødende hjørner af en firkant, dvs. Vinklerne ved siden af ​​den ene side summer op til 180 grader, så er det et parallelogram.
Hvis de indvendige ensidede vinkler lægger op til 180 grader, så er de lige linjer parallelle. Så AB er parallel med CD og BC er parallel med AD. En firkant viser sig per definition at være et parallelogram.
Sætning 29. Hvis diagonalerne på en firkant halverer hinanden i skæringspunktet, så er firkanten et parallelogram.
Bevis. Hvis AO = OC, BO = OD, så er trekanter AOD og BOC ens, da de har lige store (lodrette) vinkler ved toppunktet O, indesluttet mellem par af lige sider. Ud fra trekanters lighed konkluderer vi, at AD og BC er lige store. Siderne AB og CD er også lige store, og firkanten viser sig at være et parallelogram ifølge kriterium 1.
Sætning 30. Hvis en firkant har et par lige store parallelle sider, så er det et parallelogram.
Lad siderne AB og CD i firkant ABCD være parallelle og lige store. Lad os tegne diagonalerne AC og BD. Af parallelliteten af ​​disse linjer følger det, at de tværgående vinkler ABO = CDO og BAO = OCD er ens. Trekanter ABO og CDO er ens i sidevinkler og tilstødende vinkler. Derfor AO=OS, VO=ОD, dvs. Diagonalerne er delt i to af skæringspunktet, og firkanten viser sig at være et parallelogram ifølge kriterium 4.

I geometri overvejes specielle tilfælde af parallelogrammer.

KVADAGONER.

§43. PARALLELOGRAM.

1. Definition af et parallelogram.

Hvis vi skærer et par parallelle linjer med et andet par parallelle linjer, får vi en firkant, hvis modsatte sider er parvis parallelle.

I firkanter ABC og EFNM (fig. 224) ВD || AC og AB || CD;
EF || MN og EM || FN.

En firkant, hvis modsatte sider er parallelle i par, kaldes et parallelogram.

2. Egenskaber for et parallelogram.

Sætning. Diagonalen af ​​et parallelogram deler det i to lige store trekanter.

Lad der være et parallelogram ABC (fig. 225), hvor AB || CD og AC || ВD.

Du skal bevise, at diagonalen deler den i to lige store trekanter.

Lad os tegne diagonal CB i parallelogram ABC. Lad os bevise det /\ CAB= /\ СДВ.

Side NE er fælles for disse trekanter; / ABC = / BCD, som indre tværgående vinkler med parallelle AB og CD og sekant CB; / DIA = / СВD, også gerne indre tværgående vinkler med parallelle AC og ВD og sekant CB (§ 38).

Herfra /\ CAB = /\ СДВ.

På samme måde kan man bevise, at diagonalen AD vil dele parallelogrammet i to lige store trekanter ACD og ABD.

Konsekvenser. 1 . Modsatte vinkler af et parallelogram er lig med hinanden.

/ A = / D, dette følger af ligheden mellem trekanter CAB og CDB.
Ligeledes / C = / I.

2. Modsatte sider af et parallelogram er lig med hinanden.

AB = CD og AC = BD, da disse er sider af lige store trekanter og ligger modsat lige store vinkler.

Sætning 2. Diagonalerne i et parallelogram er delt i to ved deres skæringspunkt.

Lad BC og AD være diagonalerne af parallelogrammet ABC (fig. 226). Lad os bevise, at AO = OD og CO = OB.

For at gøre dette skal du for eksempel sammenligne et par modsat placerede trekanter /\ AOB og /\ TORSK.

I disse trekanter AB = CD, som modsatte sider af et parallelogram;
/ 1 = / 2, som indre vinkler liggende på tværs med parallelle AB og CD og sekant AD;
/ 3 = / 4 af samme grund, da AB || CD og CB er deres sekant (§ 38).

Det følger heraf /\ AOB = /\ TORSK. Og i lige trekanter ligger lige sider modsat lige store vinkler. Derfor er AO = OD og CO = OB.

Sætning 3. Summen af ​​vinklerne ved siden af ​​den ene side af et parallelogram er lig med 2 d .

Bevis det selv.

3. Tegn på et parallelogram.

Sætning. Hvis de modsatte sider af en firkant er parvis lige store, så er denne firkant et parallelogram.

Indsæt firkanten ABC (Tegnet 227) AB = CD og AC = BD. Lad os bevise, at under denne betingelse AB || CD og AC || ВD, dvs. firkantet АВDC er et parallelogram.
Lad os forbinde med et stykke et hvilket som helst to modsatte hjørner af denne firkant, for eksempel C og B. Firkanten ABCD er opdelt i to lige store trekanter: /\ CAB og /\ СДВ. Faktisk har de samme side CB, AB = CD og AC = BD alt efter tilstanden. Således er tre sider af en trekant henholdsvis lig med tre sider af en anden, derfor /\ CAB = /\ СДВ.

I lige trekanter ligger lige sider modsat lige store vinkler, Det er derfor
/ 1 = / 2 og / 3 = / 4.

Vinklerne 1 og 2 er indvendige vinkler, der ligger på tværs i skæringspunktet mellem rette linjer AB og CD på lige linje CB. Derfor AB || CD.

På samme måde er vinklerne 3 og 4 indre vinkler, der ligger på tværs i skæringspunktet mellem linjerne CA og BD på linje CB, derfor CA || ВD (§ 35).

Således er de modsatte sider af den firkantede ABC parallelle parvis, derfor er det et parallelogram, hvilket er det, der skulle bevises.

Sætning 2. Hvis to modsatte sider af en firkant er lige store og parallelle, så er firkanten et parallelogram.

Lad AB = CD og AB || CD. Lad os bevise, at under disse forhold er firkantet ABC et parallelogram (fig. 228).

Lad os forbinde toppunkterne C og B med et segment CB På grund af parallelliteten af ​​rette linjer AB og CD er vinkler 1 og 2, som indre vinkler, der ligger på tværs, lige store (§ 38).
Derefter trekant CAB lig med en trekant CDB, da de har samme side NE,
AB = CD ifølge sætningens betingelser og / 1 = / 2 ifølge bevist. Disse trekanters lighed indebærer ligheden mellem vinklerne 3 og 4, da de ligger modsat lige store sider i lige store trekanter.

Men vinklerne 3 og 4 er indre tværgående vinkler dannet af skæringspunktet mellem lige linjer AC og BD på lige linje CB, derfor AC || ВD (§ 35), dvs. en firkant
ABC er et parallelogram.

Øvelser.

1. Bevis, at hvis diagonalerne af en firkant i punktet for deres gensidige skæringspunkt er delt i to, så er denne firkant et parallelogram.

2. Bevis, at en firkant, hvis sum indvendige hjørner støder op til hver af to tilstødende sider er lig med 2 d, er der et parallelogram.

3. Konstruer et parallelogram ved hjælp af to sider og vinklen mellem dem:

a) at bruge paralleliteten af ​​modsatte sider af et parallelogram;
b) ved at bruge ligheden af ​​modsatte sider af et parallelogram.

4. Konstruer et parallelogram ved hjælp af to tilstødende sider og en diagonal.

5. Konstruer et parallelogram ved hjælp af de to diagonaler og vinklen mellem dem.

6. Konstruer et parallelogram ved hjælp af dets side og to diagonaler.