§6. ቴይለር ተከታታይ

የኃይል ተከታታዮች በግምታዊ ስሌት ውስጥ በሰፊው ጥቅም ላይ ይውላሉ. በእነሱ እርዳታ ሥሮቹን ፣ ትሪግኖሜትሪክ ተግባራትን ፣ የቁጥሮች ሎጋሪዝምን እና የተወሰኑ ውህዶችን ከተወሰነ ትክክለኛነት ጋር ማስላት ይችላሉ። የተለያዩ እኩልታዎችን ሲያዋህዱ ተከታታይም ጥቅም ላይ ይውላሉ።

1. የተግባር ዋጋዎች ግምታዊ ስሌት

በኃይል ተከታታይ ውስጥ የአንድ ተግባር መስፋፋትን አስቡበት፡-

ውስጥ የአንድ ተግባር ግምታዊ ዋጋ ለማስላት የተሰጠው ነጥብ X, የተጠቆሙ ተከታታይ convergence ክልል አባል, የመጀመሪያዎቹ በውስጡ መስፋፋት ውስጥ ይቀራሉ nአባላት ( n- የተወሰነ ቁጥር) እና የተቀሩት ውሎች ይጣላሉ

የተገኘውን ግምታዊ ዋጋ ስህተት ለመገመት, የተጣለውን ቀሪውን መገመት አስፈላጊ ነው አር n (x). ይህንን ለማድረግ የሚከተሉትን ዘዴዎች ይጠቀሙ.

ምሳሌ 1 . ተከታታይ የማስፋፊያ ኃጢአት መጠቀም x, sin20 o በ 0.0001 ትክክለኛነት ያሰሉ.

መፍትሄ. ቀመር (2) ለመጠቀም የክርክሩን ዋጋ በራዲያን መለኪያ መግለጽ አስፈላጊ ነው። እናገኛለን
. ይህንን እሴት ወደ ቀመር በመተካት, እናገኛለን

የዚህ ውጤት ተከታታዮች በምልክት ውስጥ እየተፈራረቁ ነው እና የሌብኒዝ ሁኔታዎችን ያሟላል። ምክንያቱም
, ከዚያ ይህ እና ሁሉም ተከታይ የተከታታዩ ቃላቶች ሊወገዱ ይችላሉ, እራሳችንን በመጀመሪያዎቹ ሁለት ቃላት ይገድባል. ስለዚህም

ምሳሌ 2 . አስላ
ከ 0.01 ትክክለኛነት ጋር.

መፍትሄ. ማስፋፊያውን እንጠቀም
፣ የት (በቀደመው ርዕስ ላይ ምሳሌ 5 ይመልከቱ)

ይህንን ለማድረግ ከመጀመሪያዎቹ ሶስት የማስፋፊያ ውሎች በኋላ የቀረውን መጣል እንደምንችል እንፈትሽ፡

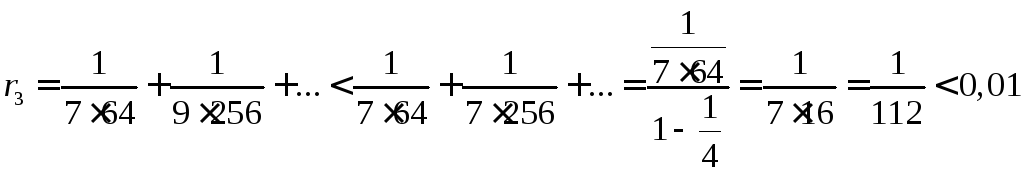ስለዚህ ይህን ቀሪውን ጥለን ማግኘት እንችላለን

ምሳሌ 3 . አስላ
ከ 0.0001 ትክክለኛነት ጋር.

መፍትሄ. የሁለትዮሽ ተከታታዮችን እንጠቀም። 5 3 የአንድ ኢንቲጀር ኩብ ወደ 130 ቅርብ ስለሆነ 130 ቁጥርን 130 = 5 3 +5 መወከል ተገቢ ነው።

የላይብኒዝ መስፈርትን ማርካት ከተፈጠረው ተለዋጭ ተከታታይ አራተኛው ቃል ከሚያስፈልገው ትክክለኛነት ያነሰ ነው።

, ስለዚህ እሱ እና የሚከተሉት ውሎች ሊወገዱ ይችላሉ.

2. የተረጋገጡ ውህዶች ግምታዊ ስሌት

በኒውተን-ላይብኒዝ ፎርሙላ ብዙ በተግባር አስፈላጊ የሆኑ የተወሰኑ ወይም ተገቢ ያልሆኑ ውህዶች ሊሰሉ አይችሉም፣ ምክንያቱም አፕሊኬሽኑ ፀረ-ተውሳሽ ከማግኘት ጋር የተያያዘ ነው፣ እሱም ብዙውን ጊዜ በአንደኛ ደረጃ ተግባራት ውስጥ መግለጫ የለውም። በተጨማሪም ፀረ-ተውጣጣ ማግኘት የሚቻል ከሆነ ይከሰታል, ነገር ግን ሳያስፈልግ ጉልበት የሚጠይቅ ነው. ነገር ግን፣ የማዋሃድ ተግባሩ ወደ ሃይል ተከታታይነት ከተዘረጋ እና የውህደት ወሰኖቹ የዚህ ተከታታይ ውህደት የጊዜ ክፍተት አባል ከሆኑ አስቀድሞ ከተወሰነ ትክክለኛነት ጋር ግምታዊ ስሌት ስሌት ማድረግ ይቻላል።

ምሳሌ 4 : የተዋሃደውን አስላ
በ 0.00001 ትክክለኛነት.

መፍትሄ. አይዛመድም። የተወሰነ ውህደት
በአንደኛ ደረጃ ተግባራት ውስጥ ሊገለጽ አይችልም, ማለትም. "ቋሚ ያልሆነ ውህደት" ይወክላል. የኒውተን-ሌብኒዝ ቀመር እዚህ ሊተገበር አይችልም። ውህደቱን በግምት እናሰላው።

የኃጢያት ተከታታዮችን ቃል በቃል መከፋፈል xላይ xእኛ እናገኛለን:

ይህንን ተከታታይ ቃል በቃሉ በማዋሃድ (ይህ ሊሆን ይችላል ፣ ምክንያቱም የውህደት ወሰኖች የዚህ ተከታታይ ውህደት የጊዜ ክፍተት ስለሆነ) ፣ እኛ እናገኛለን-

የተገኙት ተከታታይ የሊብኒዝ ሁኔታዎችን ስለሚያሟሉ እና የሚፈለገውን ዋጋ በተወሰነ ትክክለኛነት ለማግኘት የመጀመሪያዎቹን ሁለት ቃላት ድምር መውሰድ በቂ ነው.

ስለዚህ, እናገኛለን

ምሳሌ 5 . የተዋሃደውን አስላ ከ 0.001 ትክክለኛነት ጋር.

ከተከታታዩ ተከታታይ ሁለተኛ ጊዜ በኋላ ቀሪውን መጣል እንደምንችል እንፈትሽ።

ስለዚህም እ.ኤ.አ.
.

የተወሰነ የተወሰነ $\int\limits_(a)^(b)f(x)dx$ ከተወሰነ ትክክለኛነት $\varepsilon$ ጋር ማስላት አስፈላጊ ይሁን። የ$f(x)$ አንቲደርቭቲቭ ኢንተግራንድ ተግባርን በቀጥታ ማግኘት በጣም አዳጋች ከሆነ ወይም ዋናው $\int f(x)dx$ ጨርሶ ካልተወሰደ፣ በነዚህ አጋጣሚዎች ተግባራዊ ተከታታይ መጠቀም ይችላሉ። በተለይም የማክላሪን ተከታታይ ጥቅም ላይ ይውላሉ, በእሱ እርዳታ የተግባር $ f (x) $ ውህደት የኃይል ተከታታይ መስፋፋት ተገኝቷል. ለዚያም ነው በስራችን ውስጥ ከማክላሪን ተከታታይ ጋር አንድ ሰነድ ያስፈልገናል.

የምንጠቀመው የኃይል ተከታታዮች አንድ ወጥ በሆነ መልኩ ይሰባሰባሉ፣ ስለዚህ በመካከላቸው ባለው ክፍተት ውስጥ ካለ ማንኛውም ክፍል ላይ በቃል ሊዋሃዱ ይችላሉ። ተከታታይን በመጠቀም የመዋሃድ ስሌትን የሚያካትት ተመሳሳይ ችግሮችን ለመፍታት እቅድ ቀላል ነው-

ውህደቱን ወደ ተግባራዊ ተከታታይ (አብዛኛውን ጊዜ የማክላሪን ተከታታይ) ዘርጋ።
በመጀመሪያው አንቀጽ ላይ የተጻፉትን የተግባር ተከታታዮች የውል ቃል-በ-ጊዜ ውህደትን ያከናውኑ።
በሁለተኛው አንቀጽ ውስጥ የተቀበለውን መጠን አስሉ ተከታታይ ቁጥርበተሰጠው ትክክለኛነት $ \ varepsilon $.

ተከታታይን በመጠቀም የመገጣጠሚያዎች ስሌትን የሚያካትቱ ችግሮች በከፍተኛ ሂሳብ ውስጥ ባሉ መደበኛ ስሌቶች አዘጋጆች ዘንድ ታዋቂ ናቸው። ስለዚህ ፣ በዚህ ርዕስ ውስጥ አምስት ምሳሌዎችን እንመረምራለን ፣ በእያንዳንዳቸው ውስጥ ከ $ \ varepsilon $ ትክክለኛነት ጋር የተወሰነ ውህደትን ማስላት ያስፈልገናል።

ምሳሌ ቁጥር 1

$\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx$ ትክክለኛ ወደ $\varepsilon=10^(-3)$ አስላ።

ዋናው $\int e ^ (-x^2) dx$ እንዳልተወሰደ ወዲያውኑ እናስተውል፣ ማለትም። የመዋሃዱ ፀረ-ተውጣጣው በመጨረሻው የአንደኛ ደረጃ ተግባራት ጥምረት አልተገለጸም. በሌላ አነጋገር መደበኛ ዘዴዎችን በመጠቀም (መተካት ፣ በክፍሎች መቀላቀል ፣ ወዘተ) የተግባር ፀረ-ተውጣጣ$e^(-x^2)$ ሊገኝ አይችልም።

ለእንደዚህ አይነት ስራዎች ሁለት የንድፍ አማራጮች አሉ, ስለዚህ ለየብቻ እንመለከታቸዋለን. በተለምዶ, "የተስፋፋ" እና "አጭር" ስሪቶች ተብለው ሊጠሩ ይችላሉ.

የተዘረጋ የንድፍ አማራጭ

የማክላሪን ተከታታይ

$$e^x=1+x+\frac(x^2)(2)+\frac(x^3)(6)+\ldots$$

$$e^(-x^2)=1-x^2+\frac(\ግራ(-x^2\ቀኝ)^2)(2)+\frac(\ግራ(-x^2\ቀኝ) ^3)(6)+\ldots=1-x^2+\frac(x^4)(2)-\frac(x^6)(6)+\ldots$$

የተፈጠረውን መስፋፋት በ$\ግራ$ መካከል እናዋህዳለን፡-

$$\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx=\int\limits_(0)^(\frac(1)(2))\ግራ (1-x^2+\frac(x^4)(2)-\frac(x^6)(6)+\ldots\ቀኝ)dx=\\ =\ግራ።\ግራ(x-\frac() x^3)(3)+\frac(x^5)(10)-\frac(x^7)(42)+\ldots\ቀኝ)\ቀኝ|_(0)^(1/2)= \ frac(1)(2)-\frac(1)(3\cdot(2^3))+\frac(1)(10\cdot(2^5))-\frac(1)(42\cdot) 2^7))+\ldots$$

የተለዋዋጭ ተከታታዮች ተያያዥ ምልክት አግኝተናል። ይህ ማለት የአንድ የተወሰነ ውህደት ግምታዊ ዋጋ ለማስላት $k$ የውጤቱን ተከታታይ ውሎች ከወሰድን ስህተቱ ከተከታታዩ $(k+1)$ ኛ ሞጁል አይበልጥም።

እንደ ሁኔታው ትክክለኛነት $\varepsilon=10^(-3)$ ነው። ከ$\frac(1)(42\cdot(2^7))=\frac(1)(5376) ጀምሮ<10^{-3}$, то для достижения требуемой точности достаточно ограничиться первыми тремя членами знакочередующегося ряда:

$$\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx\approx\frac(1)(2)-\frac(1)(3\cdot() 2^3))+\frac(1)(10\cdot(2^5))=\frac(443)(960)።$$

የተገኘው የእኩልነት ስህተት ከ$\frac(1)(5376)$ አይበልጥም።

ሆኖም ተራ ክፍልፋዮችን ማጠቃለል በጣም አድካሚ ሥራ ነው ፣ ስለሆነም ብዙውን ጊዜ ስሌቶች በአስርዮሽ ክፍልፋዮች ይከናወናሉ

$$\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx\approx\frac(1)(2)-\frac(1)(3\cdot() 2^3))+\frac(1)(10\cdot(2^5))\ግምታዊ(0(,)5)-0(,)0417+0(,)0031\approx(0(,)461 )$$

እርግጥ ነው, በዚህ ጉዳይ ላይ የማዞሪያ ስህተት ግምት ውስጥ መግባት አለበት. የመጀመሪያው ቃል (ማለትም $0(፣)5$) በትክክል ተሰላ ነበር፣ ስለዚህ እዚያ ምንም የማጠጋጋት ስህተት የለም። ሁለተኛው እና ሶስተኛው ቃላቶች ወደ አራተኛው የአስርዮሽ ቦታ ተወስደዋል, ስለዚህ ለእያንዳንዳቸው የማዞሪያ ስህተት ከ $ 0.0001 ዶላር አይበልጥም. የተገኘው የማጠጋጋት ስህተት ከ$0+0(,)0001+0(,)0001=0(,)0002$ አይበልጥም።

ስለዚህ፣ አጠቃላይ የእኩልነት ስህተት $\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx\approx(0(,)461)$ ከ$0 አይበልጥም። (፣)0002 +\frac(1)(5376)<10^{-3}$, т.е. значение интеграла вычислено с требуемой точностью.

የንድፍ አጠር ያለ ስሪት

የ$e^x$ ተግባርን በማክላሪን ተከታታይ እንፃፍ፡-

$$e^x=\ ድምር\liits_(n=0)^(\infty)\frac(x^n)(n)$$ !}

ይህ ማስፋፊያ ለሁሉም $x\in(R)$ የሚሰራ ነው። ከ$x$ ይልቅ $-x^2$ን እንተካ፡

$$e^(-x^2)=\ ድምር \ ገደብ_(n=0)^(\infty)\frac(\ግራ(-x^2\ቀኝ)^n)(n)=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}$$ !}

ውጤቱን በተከታታይ በ$\ግራ$ ላይ እናዋህዳለን፡-

$$\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx=\int\limits_(0)^(\frac(1)(2))\sum \liits_(n=0)^(\infty)\frac((-1)^n\cdot(x)^(2n))(ndx= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\int\limits_{0}^{\frac{1}{2}}x^{2n}dx=\\ =\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\left.\frac{x^{2n+1}}{2n+1}\right|_{0}^{1/2}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot\left(\frac{1}{2}\right)^{2n+1}}{n!\cdot(2n+1)}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}$$ !}

$$\sum\limits_(n=0)^(\infty)\frac(-1)^n)(n!\cdot(2n+1)\cdot(2^(2n+1))))=\ frac(1)(2)-\frac(1)(24)+\frac(1)(320)-\frac(1)(5376)+\ldots$$

በተስፋፋው የንድፍ እትም ውስጥ ስህተቶችን በተመለከተ የተደረጉ ሁሉም አስተያየቶች ልክ እንደሆኑ ይቆያሉ, ማለትም. $\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx\approx\frac(1)(2)-\frac(1)(3\cdot(2) ^3))+\frac(1)(10\cdot(2^5))\ግምት(0(,)461)$።

የአጭር ጊዜ ቅጂው ከተስፋፋው ለምን ይሻላል?

በመጀመሪያ ፣ የተወሰነውን ውህድ ከተወሰነ ትክክለኛነት ጋር ለማስላት በዋናው ማስፋፊያ ውስጥ ምን ያህል የተከታታዩ ውሎች እንደሚወስዱ መገመት አያስፈልገንም። ለምሳሌ፣ በመፍትሔው መጀመሪያ ላይ ጽፈናል፡-

$$e^(-x^2)=1-x^2+\frac(x^4)(2)-\frac(x^6)(6)+\ldots$$

ሆኖም ግን፣ ተከታታይ የሆኑትን አራት ቃላት በትክክል መውሰድ እንዳለብን ለምን ወሰንን? ሁለት ተከታታይ አባላትን ወይም አምስትን ወይም መቶዎችን መውሰድ ቢያስፈልግስ? የተከታታዩ ስድስተኛው ቃል ብቻ ከ$\varepsilon$ ያነሰ ሆኖ ከተገኘ፣ ታዲያ ምን? እና ከዚያ ወደ የመፍትሄው መጀመሪያ ተመለስን ፣ ተጨማሪ ሁለት ተከታታይ ውሎችን ጨምር እና እነሱን ማዋሃድ አለብን። እና ይህ በቂ ካልሆነ, ይህን አሰራር እንደገና ያድርጉ.

የአህጽሮት ቀረጻው እንደዚህ አይነት ችግር አይገጥመውም. የቁጥር ተከታታዮች በአጠቃላይ መልክ ተጽፎ እናገኛለን፣ ስለዚህም እንደ አስፈላጊነቱ ብዙ አባላቱን መውሰድ እንችላለን።

ከላይ በተጠቀሱት ምክንያቶች መሰረት, አጭር የመቅዳት ዘዴን እመርጣለሁ. ለወደፊቱ, በዚህ ርዕስ ውስጥ ሁሉም ውሳኔዎች በአህጽሮት መልክ ይቀርባሉ.

መልስ: $\int\limits_(0)^(\frac(1)(2))e^(-x^2)dx\approx(0(,)461)$።

ምሳሌ ቁጥር 2

የተወሰነውን $\int\limits_(0)^(0(,)2)\frac(1-\cos\frac(5x)(3))(x)dx$ ትክክለኛ ወደ $\varepsilon=10^() አስላ። -3)$፣ ውህደቱን ወደ ማክላሪን ተከታታይ በማስፋት እና ቃልን በቃል በማዋሃድ።

የማክላሪን ተከታታይ $\frac (1-\cos\frac(5x)(3))(x)$ን በማስፋፋት እንጀምር። በማክላሪን ተከታታይ የ$\cos(x)$ ተግባር መስፋፋትን እንፃፍ፡-

$$\cos(x)=\ ድምር \ ገደብ_(n=0)^(\infty)\frac((-1)^n\cdot(x)^(2n))(2n)$$ !}

ይህ ማስፋፊያ ለሁሉም $x\in(R)$ የሚሰራ ነው። ክፍልፋይ $\frac(5x)(3)$ን ከ$x$ እንተካ፡

$$\cos(\frac(5x)(3))=\ደምር\liits_(n=0)^(\infty)\frac(-1)^n\cdot(\ግራ(\frac(5x) 3)\ቀኝ))^(2n))((2n)= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}.$$ !}

አሁን $1-\cos\frac(5x)(3)$ን እናስፋፋ።

$$ 1 - \ cos \ frac (5x) (3) = 1 - \ ድምር \ ገደቦች_(n=0) ^ (\ infty) \ frac ((-1) ^ n\cdot(5^(2n))\ cdot(x)^(2n))(3^(2n)\cdot((2n)} $$ !}

ከ $\ sum\limits_(n=0)^(\infty)\frac((-1)^n\cdot(5^(2n))\cdot(x)^(2n))(3^) በመውሰድ ላይ (2n) \cdot((2n)}$ первый член, получим: $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$. Следовательно:!}

$$ 1-\ sum\limits_(n=0)^(\infty)\frac(-1)^n\cdot(5^(2n))\cdot(x)^(2n))(3^(2n))(3^() 2n) \cdot((2n)}=1-\left(1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}\right)=\\ =-\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} =\sum\limits_{n=1}^{\infty}\frac{-(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}. $$ !}

የቀረው የመጨረሻው ነገር በ$x$ መከፋፈል ነው።

$$ \frac(1-\cos\frac(5x)(3))(x)=\frac(1)(x)\cdot\sum\limits_(n=1)^(\infty)\frac(( -1)^(n+1)\cdot(5^(2n))\cdot(x)^(2n))(3^(2n)\cdot((2n))}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}. $$ !}

ይህንን ማስፋፊያ በ$\ግራ$ መካከል እናዋህደው፡-

$$ \int\limits_(0)^(0(,)2)\frac(1-\cos\frac(5x)(3))(x)dx=\int\limits_(0)^(\frac() 1)(5))\ ድምር \liits_(n=1)^(\infty)\frac((-1)^(n+1)\cdot(5^(2n))\cdot(x)^(2n) -1))(3^(2n)\cdot((2n)}dx= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\int\limits_{0}^{\frac{1}{5}}{x}^{2n-1}dx=\\ =\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\cdot\left.\frac{x^{2n}}{2n}\right|_{0}^{1/5}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}} $$ !}

ለተለዋጭ ረድፍ ምልክት ደርሰናል። የዚህን ተከታታይ የመጀመሪያዎቹን ጥቂት ውሎች እንፃፍ (የፅሁፍ ቃሉ ከ$\varepsilon$ እስኪቀንስ ድረስ)፡-

$$\sum\limits_(n=1)^(\infty)\frac(-1)^(n+1))((2n)\cdot 3^(2n)\cdot((2n)}=\frac{1}{36}-\frac{1}{7776}+\ldots$$ !}

ከ$\frac(1)(7776) ጀምሮ<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первого члена полученного числового ряда:

$$\int\limits_(0)^(0(,)2)\frac(1-\cos\frac(5x)(3))(x)dx\approx\frac(1)(36)\ግምታዊ( 0(,)028)$$

መልስ: $\int\limits_(0)^(0(,)2)\frac(1-\cos\frac(5x)(3))(x)dx\approx(0(,)028)$።

የማክላሪን ተከታታዮችን በመጠቀም ውህደቶችን የማስላት ርዕስ እንቀጥላለን

እዚህ በቀድሞው አንቀፅ ውስጥ በተሰጡት የኃይል ተከታታይ ተግባራት ውስጥ መስፋፋትን ግምት ውስጥ ማስገባት ጠቃሚ ነው ሠ x፣ shx፣ chx፣ six፣ cosx፣ (1+x) m ፣ ln(1+x)፣ arcgx።

ሎጋሪዝምን ለማስላት ውጤታማ ቀመር ነው

በእኩልነት በቀኝ በኩል ያለው ተከታታይ በፍጥነት ይሰበሰባል፣ የበለጠ ቲ.

የተግባሩን ግምታዊ ዋጋ ለማስላት ረ(x)ወደ ኃይል ተከታታይነት በመስፋፋቱ የመጀመሪያዎቹ ተጠብቀዋል nአባላት (ገጽ-የመጨረሻ እሴት) እና የተቀሩት ውሎች ተጥለዋል። የተገኘውን የተጠጋ እሴት ስህተት ለመገመት የተጣሉ ቃላት ድምርን መገመት አስፈላጊ ነው. የተሰጠው ተከታታይ ቋሚ ምልክት ከሆነ፣ ተከታታይ የተጣሉ ቃላትን ያቀፈው ወሰን በሌለው ጂኦሜትሪክ እድገት ጋር ይነጻጸራል። በተለዋጭ ተከታታዮች ውስጥ አባላቱ የላይብኒዝ መስፈርትን ያሟሉ, ግምቱ ጥቅም ላይ ይውላል < ከተከታታዩ የተጣሉ ውሎች ውስጥ የመጀመሪያው የት አለ.

403.

0 < x < n+1

∆ የዚህ ግምታዊ እኩልነት ስህተት የሚወሰነው በሚከተለው ቃላቶች ድምር ነው። x p/p!በመበስበስ ላይ ሠ x:

እያንዳንዱን ምክንያቶች መተካት n+2፣ n+3፣ n+4፣...አነስተኛ ዋጋ n+1, እኩልነትን እናገኛለን

እነዚያ። ▲

404 . በጣም ቅርብ ወደሆነው 0.00001 አስላ።

∆ ማስፋፊያውን በመጠቀም ሠ xበተከታታይ, እናገኛለን

ቁጥሩን እንወስን nስለዚህ የግምታዊ እኩልነት ስህተት

ከ 0.00001 አይበልጥም. ባለፈው ምሳሌ የተሰጠውን የስህተት ግምት እንጠቀም። እናምናለን። x=1/2; ከዚያም

እነዚያ።

በምርጫ የምንወስነው በምን አይነት እሴት ነው n እኩልነት የሚሟላው። አር ፒ< 0.00001. ለምሳሌ ያህል፣ n= 3, እናገኛለን አር 3< 1/ (8 6 7) , ማለትም አር 3< 1/336. እናድርግ ፣ የበለጠ ፣ n=5; ከዚህ አር 5< 1/(32·120·11), ማለትም አር 5< 1/42240. በመጨረሻ ፣ n= 6; ከዚህ አር 6< 1/(64·720·13) ፣ ማለትም እ.ኤ.አ. አር 6< 1/100000. ስለዚህ እንቀበል n= 6:

ውሎቹን እናጠቃልለው፡-

0.020833 (ከቀዳሚው ጊዜ 6 እጥፍ ያነሰ)
0.002604 ("8""")

0.000260 (" 10 "" "")

0.000022 (" 12 "" "")

ማለት፣ እያንዳንዱን ቃል በ 0.000001 ትክክለኛነት እናሰላለን, ስለዚህ በማጠቃለያ ጊዜ ከ 0.00001 በላይ ስህተት እንዳንገኝ.

405. በትክክለኛነት ወደ 0.00001 አስሉ.
∆ አለን።

ግምታዊውን እኩልነት እንጠቀም

ተለዋጭ ተከታታይ የላይብኒዝ መስፈርት ሁኔታዎችን ስለሚያረካ 5 ውሎችን ወስደናል፣ እና ስለዚህ በፍፁም ዋጋ ያለው የሚፈቀደው ስህተት ከተከታታዩ የተጣሉ ውሎች የመጀመሪያ ያነሰ መሆን አለበት። የወደቀው የመጀመሪያው ቃል 1/(5!5 5) ነው። ያንን ማየት ቀላል ነው 1/(5!5 5)< 0,00001.

ስሌቶቹን ካከናወኑ በኋላ ውጤቱ ነው . ▲

406. መበስበስን በመጠቀም ኮስክስበአንድ ረድፍ, አስላ сos 18 °ከ 0.0001 ትክክለኛነት ጋር.

сos 18°= ;

ከ (1/6!) - (π/10) 6 ጀምሮ ሶስት ተከታታይ ቃላትን መውሰድ በቂ ነው< 0,0001. Тогда

. ▲

407. በጣም ቅርብ ወደሆነው 0.0001 አስላ።

∆ ማስፋፊያውን እንጠቀም (1+x) ሜትርበማሰብ በተከታታይ x = 0.1፣ m=1/5.

አራተኛው ጊዜ ከ 0.0001 ያነሰ ስለሆነ አራተኛውን እና ተከታዩን ውሎች እናስወግዳለን. ስለዚህ፣ ▲

408. በጣም ቅርብ ወደሆነው 0.001 አስላ።

∆ 5 3 የኢንቲጀር ኩብ ለቁጥር 130 ቅርብ ስለሆነ 130 ቁጥርን እንደ የሁለት ቃላት ድምር አድርጎ መወከል ተገቢ ነው፡ 130 = 5 3 + 5. ከዚያም

አራተኛው ቃል ከ 0.001 ያነሰ ነው, ስለዚህ እሱ እና ከእሱ በታች ያሉት ውሎች ሊወገዱ ይችላሉ. ስለዚህ, 5 + 0.0667-0.0009, ማለትም 5.066. ▲

409. ln1.04ን ወደ 0.0001 አስላ።
∆ የማስፋፊያውን ln (1+.) እንጠቀም x) በተከታታይ፡-

ከየት ነው ln1.04≈ 0.0392. ▲

410. በትክክለኛው ትሪያንግል ውስጥ እግሮቹ ከ 1 እና 5 ሴ.ሜ ጋር እኩል ናቸው ከትንሽ እግር ተቃራኒው የተኛን ትሪያንግል አንግል በትክክል 0.001 ራዲያን።

∆ ከ tanα=1/5፣ ከዚያ α=arctg(1.5)። ማስፋፊያውን እንጠቀም

ከየት ነው α ≈ 0.2-0.0027, ማለትም α ≈ 0.197. ▲

411. የግምታዊ እኩልነት ስህተትን ይገምቱ

∆ ችግሩ የሚመጣው የተቀሩትን ተከታታዮች ድምር ለመገመት ነው።

እያንዳንዳቸውን 2n+3፣ 2n + 5፣ 2n+7፣ ... በትንሽ ቁጥር 2n+1 በመተካት እኩልነትን እናገኛለን።

ወሰን በሌለው መልኩ እየቀነሰ ያለውን የጂኦሜትሪክ እድገት በካሬ ቅንፎች ውስጥ እናጠቃልለው፡-

እነዚያ። ▲

412. ln2ን ወደ ቅርብ 0.0001 አስላ።

∆ ln (t + 1) እና ለመገመት አለመመጣጠን ለመወሰን በቀመር ውስጥ አር ፒብለን እናምናለን። t= 1:

በምርጫ እንወስናለን። nእኩልነት እንዲይዝ አር.ኤን< 0,0001. n=2 ከሆነ እንግዲያውስ አር 2< 1/(4∙5∙3 3); አር 2< 1/540; n = 3 ከሆነ ፣ ከዚያ R 3< 1(4∙7∙3 5); R 3 < 1/6804; если n= 4, то አር 4< 1/(4∙9∙3 7); አር 4 < 1/10000.

ስለዚህ, n = 4 እና ln 2 ን ለማስላት ግምታዊውን እኩልነት እናገኛለን
በ arcg x መስፋፋት.

ያገኘናቸውን ልዩ ማስፋፊያዎች እንደ ምሳሌ በመጠቀም፣ ገደብ የለሽ ተከታታይ ግምታዊ ስሌቶችን እንዴት መጠቀም እንደሚቻል እናብራራለን። ከብዙ አጠቃላይ አስተያየቶች ጋር እንጀምር።

ያልታወቀ ቁጥር A ወደ ተከታታይ ከተስፋፋ፡-

በቀላሉ የሚሰሉ (ብዙውን ጊዜ ምክንያታዊ) ቁጥሮች የት ናቸው ፣ እና በግምት እናስቀምጣለን-

ከዚያም ሁሉንም ሌሎች ቃላትን ለመጣል የሚደረገው እርማት በቀሪው ይገለጻል

በቂ መጠን ሲኖረው፣ ይህ ስህተት በዘፈቀደ ትንሽ ይሆናል፣ ስለዚህም በማንኛውም አስቀድሞ ከተወሰነ ትክክለኛነት ጋር ይባዛል።

የቀረውን በቀላሉ የመገመት ችሎታ ላይ ፍላጎት አለን ፣ ይህም የሚፈለገውን ትክክለኛነት ግምት ውስጥ በማስገባት ተከታታይ ከፊል ድምር ሲሰላ በጊዜ ለማቆም ያስችለናል።

እየተገመገመ ያለው ተከታታዮች በምልክት ውስጥ ተለዋጭ ከሆኑ እና በተጨማሪም ፣ በቃላቶች በፍፁም እሴት (“የዘይብኒትዝ ዓይነት”) እየቀነሱ ከሄዱ ፣ እንደተመለከትነው ፣ ቀሪው የመጀመሪያ ቃል ምልክት አለው እና በ ውስጥ ያነሰ ነው። ፍጹም ዋጋ. ይህ ግምገማ ከቀላልነት አንፃር ብዙ የሚፈለግ አይደለም።

በአዎንታዊ ተከታታይ ሁኔታ ሁኔታው በተወሰነ ደረጃ የተወሳሰበ ነው።

ከዚያም አብዛኛውን ጊዜ በቀላሉ ሊጠቃለል የሚችል አወንታዊ ተከታታይ ለማግኘት ይሞክራሉ, ቃላቱ ከእኛ ፍላጎት ከተቀረው ውል የበለጠ ይሆናል, እና ቀሪውን በዚህ ተከታታይ ድምር ይገምታሉ.

ለምሳሌ ፣ ለተከታታይ - የሚከተሉትን ማግኘት ይችላሉ-

[ይህ ግምት በ 373 (11) ውህደትን በመጠቀም ከተገኘው ከፍተኛ ግምት ጋር ይዛመዳል] እና ለተከታታዩ

[በእውነቱ የ37ቱን ቁጥር ስናሰላ ይህንን ግምት ተጠቅመንበታል።

ብዙውን ጊዜ፣ የቁጥር A አስርዮሽ መጠጋጋት ያስፈልጋል፣ የተከታታዩ ቃላቶች ግን በአስርዮሽ ክፍልፋዮች ላይገለጹ ይችላሉ። እነሱን ወደ አስርዮሽ ክፍልፋይ ሲቀይሩ፣ እነሱን ማጠጋጋት አዲስ ስህተት ይፈጥራል እናም ግምት ውስጥ መግባት አለበት።

በመጨረሻም ፣ እኛ የምንፈልገው ቁጥር ሀ ያለው ድምር ያለው እያንዳንዱ ተከታታይ ይህንን ቁጥር በትክክል ለማስላት ተስማሚ እንዳልሆነ እናስተውላለን (ምንም እንኳን ቃላቱ ቀላል እና የቀረውን መገመት ቀላል ቢሆንም)። ጥያቄው የመገጣጠም ፍጥነት ነው, ማለትም, ከፊል ድምር ወደ ቁጥር A የሚቀርብበት ፍጥነት.

ለምሳሌ ረድፎችን እንውሰድ [ተመልከት. 404 (16) እና 405 (18)፡

መስጠት, በቅደም, ቁጥሮች መበስበስ - እና እነዚህን ቁጥሮች ያላቸውን እርዳታ ጋር ለማስላት, እስከ ትክክለኛነት ጋር, በላቸው, በመጀመሪያው ጉዳይ ላይ አምሳ ሺህ ቃላት እና በሁለተኛው ውስጥ አንድ መቶ ሺህ ቃላት መጨመር አስፈላጊ ነበር; ይህ በእርግጥ የሚቻለው በከፍተኛ ፍጥነት ባላቸው ኮምፒተሮች እርዳታ ብቻ ነው።

ከዚህ በታች የተጠቀሱትን ቁጥሮች በበለጠ ትክክለኛነት እንኳን በቀላሉ እናሰላለን, ነገር ግን ይበልጥ ተስማሚ ራዲሎችን በመጠቀም.

ትምህርት 57

ተግባራትን ወደ ኃይል ተከታታይ ማስፋፋት።

በክፍለ-ጊዜው ውስጥ ማለቂያ የሌለው ልዩነት ያለው ማንኛውም ተግባር, ማለትም.
, በዚህ የጊዜ ክፍተት ውስጥ ከእሱ ጋር የሚገጣጠም ማለቂያ ወደሌለው የኃይል ህግ ሊሰፋ ይችላል ቴይለር ተከታታይ

ሁኔታው በዚህ ክፍተት ውስጥ ከተሟላ
፣ የት
የቴይለር ቀመር ቀሪ ቃል ነው።

በ
የሚባሉትን እናገኛለን የማክላሪን ተከታታይ:.

በአንዳንድ ክፍተቶች ውስጥ ነጥብ የያዘ ከሆነ ፣ ለማንኛውም እኩልነት ይይዛል
፣ የት
አዎንታዊ ቋሚ ነው, እንግዲህ
እና ተግባር
ወደ ቴይለር ተከታታይ እናስፋፋው።

የሚከተሉትን ተግባራት የቴይለር ተከታታይ ማስፋፊያዎችን እናቅርብ።

8) ሁለትዮሽ ተከታታይ;

ይህ የመጨረሻው መስፋፋት በሚከተሉት ሁኔታዎች ውስጥ ተግባራዊ ይሆናል:

በ
ከሆነ

በ
ከሆነ
.

በአጠቃላይ ተግባራትን ወደ ሃይል ተከታታይ ማስፋፋት በቴይለር ወይም በማክላሪን ተከታታይ አጠቃቀም ላይ የተመሰረተ ነው. በተግባራዊ መልኩ፣ ተከታታይ (1-8) ወይም የጂኦሜትሪክ ግስጋሴ ቃላት ድምር ቀመር በመጠቀም የበርካታ ተግባራት የሃይል ተከታታዮች በመደበኛነት ሊገኙ ይችላሉ። አንዳንድ ጊዜ በሚበሰብስበት ጊዜ የቃል-በ-ጊዜ ልዩነት ወይም ተከታታይ ውህደት መጠቀም ጠቃሚ ነው. በመገጣጠሚያው ክፍተት ውስጥ, ተከታታዮቹ ወደ ተጓዳኝ ተግባራት ይሰበሰባሉ.

1. የልዩነት ኃይሎችን ዘርጋ
ተግባር
.

መፍትሄ። የቴይለርን ቀመር ለመጠቀም
, እናገኛለን:

ወዘተ.

ስለዚህም እ.ኤ.አ.

2. ተኛ
በስልጣኖች ቅደም ተከተል
.

መፍትሄ። እኩልነቱን እንጠቀም
. የዚህ እኩልነት የቀኝ ጎን ከመጀመሪያው ቃል ጋር ያለማቋረጥ እየቀነሰ የጂኦሜትሪክ እድገት ድምር ተደርጎ ሊወሰድ ይችላል።
እና አካታች
. ከዚህ እናገኛለን

ምክንያቱም
፣ ያ

3. በማክላሪን ተከታታይ ውስጥ ያለውን ተግባር ያስፋፉ

መፍትሄ። ይህንን ተግባር ወደ ቀላል ምክንያታዊ ክፍልፋዮች ድምር እንዘርጋው፡-

ጀምሮ

ያ

ከተከታታዩ ጀምሮ
ላይ ይሰበሰባል
, እና ተከታታይ
ላይ ይሰበሰባል
, ከዚያም ተከታታይ
መቼ ወደዚህ ተግባር ይቀላቀላል
.

4. ተግባሩን ወደ ኃይል ተከታታይ ዘርጋ
.

መፍትሄ። የተግባሩን እና ተዋጽኦዎቹን እሴቶች በ ላይ እናገኛለን

ምክንያቱም
, ከዚያም ለቋሚ እኩልነት አለ
በማንኛውም . ስለዚህ፣ ተግባሩ እንደ ቴይለር ተከታታይ ድምር ሊወከል ይችላል።

በዚህ ጉዳይ ላይ

ይህ መስፋፋት በሌላ መንገድ ሊገኝ ይችላል-በማስፋፋቱ ውስጥ በቂ ነው
መተካት ላይ
.

5. ተግባሩን ወደ ኃይል ተከታታይ ዘርጋ

.

መፍትሄ። በመበስበስ ላይ

መተካት ላይ
, እናገኛለን

6. አስቀምጡ
በስልጣኖች ቅደም ተከተል
.

መፍትሄ። በመበስበስ ላይ

መተካት ላይ
, እናገኛለን

7. ተግባሩን ወደ ኃይል ተከታታይ ዘርጋ
.

መፍትሄ። መሆኑን አስተውል
.ተከታታዩን አስቡበት

ይህ ተከታታይ በ ላይ ይሰበሰባል
, ይህም ማለት በማንኛውም የጊዜ ክፍተት በቃል ሊዋሃድ ይችላል
. ስለዚህም እ.ኤ.አ.

፣ ማለትም ፣ ከዚህ ተግባር ጋር የሚጣመር ተከታታይ በ

8. በዲግሪዎች ያዘጋጁ
ፖሊኖሚል

9. በዲግሪዎች ያዘጋጁ
ተግባር
እና የተከታታይ ተከታታዮች የመገጣጠም ክልልን ያግኙ።

መልስ፡-

10. በዲግሪዎች ያዘጋጁ
ተግባር
እና የዚህን ተከታታይ መጋጠሚያ ክልል ያግኙ።

11. በዲግሪዎች ያዘጋጁ
ተግባር
. የዚህ ተከታታይ መጋጠሚያ ክልልን ያግኙ።

መልስ

በማክላሪን ተከታታይ ውስጥ ያለውን ተግባር ያስፋፉ
. የዚህ ተግባር የውጤት ተከታታዮች መጋጠሚያ ክልልን ያመልክቱ።

12.
.

13.
መልስ፡-
.

14.
መልስ፡-
.

15.
መልስ፡-

16.
መልስ፡-
.

17.
መልስ፡-
.

18.
መልስ፡-

19.
. መልስ፡-
.

መልስ፡-

6.16. በግምታዊ ስሌቶች ውስጥ የኃይል ተከታታይ ትግበራየተግባር እሴቶችን ማስላት
. የአንድ ተግባር የኃይል ተከታታይ ይስጥ
. የዚህን ተግባር ዋጋ የማስላት ተግባር ለተወሰነ የክርክር እሴት የተከታታይ ድምርን ማግኘት ነው። እራሳችንን ለተከታታዩ የተወሰኑ የቃላት ብዛት በመገደብ የተግባርን ዋጋ የምናገኘው የቀረውን ተከታታይ ቁጥር ወይም የቀረውን ቃል በመገመት ሊቋቋም በሚችል ትክክለኛነት ነው።
፣ የት
የቴይለር ወይም የማክላሪን ቀመሮች። የተሰጠው ተከታታይ ቋሚ ምልክት ከሆነ፣ ተከታታይ የተጣሉ ቃላትን ያቀፈው ወሰን በሌለው ጂኦሜትሪክ እድገት ጋር ይነጻጸራል። በተለዋጭ ተከታታይ ሁኔታ, ግምቱ ጥቅም ላይ ይውላል

- ከተጣሉት ተከታታይ አባላት የመጀመሪያው.

ምሳሌ 1. የ ln1.1 ዋጋን በ 0.0001 ትክክለኛነት አስሉ.

መፍትሄ።

የአንድ ተግባር ግምታዊ ዋጋዎችን ከተወሰነ ትክክለኛነት ጋር ለማስላት ፣ ተጓዳኝ ተከታታዮች በምልክት ውስጥ ሲቀያየሩ በጉዳዩ ውስጥ ተከታታይ ለመጠቀም ምቹ ነው ። ለተለዋዋጭ ተከታታይ ተከታታይ የድምሩ ግምታዊ ዋጋ ስህተት ለመገመት ቀላል ነው - ከተጣሉት ቃላቶች የመጀመሪያ ፍፁም ዋጋ ያነሰ ነው።

ለተግባሩ ln(1+x) ተከታታይ እንውሰድ፡-

የዚህ ተከታታይ አራተኛ ቃል ፍፁም ዋጋ ከ 0.0001 ያነሰ ነው። ስለዚህ, በተለዋዋጭ convergent ተከታታይ ንብረት መሰረት, ln1,1 ግምታዊ ዋጋን በ 0.0001 ትክክለኛነት ለማስላት, የተከታታዩ የመጀመሪያዎቹን ሶስት ቃላት ድምርን መውሰድ በቂ ነው.

ትክክለኛነት፡ 0.001.

በተተገበሩ ችግሮች ውስጥ, የተጠጋጋ ስህተት ግምት አስፈላጊ ነው.

ፍቺ: የስሌቱ ትክክለኛነት ከተከታታዩ የተጣሉ ንጥረ ነገሮች ውስጥ ከመጀመሪያው አይበልጥም.

1.የግምታዊ እኩልነት ስህተትን ይገምቱ

መፍትሄ። የዚህ ግምታዊ እኩልነት ስህተት የሚወሰነው በሚከተለው ቃላቶች ድምር ነው።
በመበስበስ ላይ :

እያንዳንዱን ምክንያቶች መተካት
፣ ትንሽ እሴት
, እኩልነትን እናገኛለን

ወሰን በሌለው መልኩ እየቀነሰ ያለውን የጂኦሜትሪክ ግስጋሴ እናጠቃልለው፡-

፣ ማለትም እ.ኤ.አ.

2. አስላ
በ 0.00001 ትክክለኛነት.

መፍትሄ። መበስበስን በመጠቀም በተከታታይ, እናገኛለን

ቁጥሩን እንወስን ስለዚህ የግምታዊ እኩልነት ስህተት

ከ 0.00001 አይበልጥም. ባለፈው ምሳሌ የተሰጠውን የስህተት ግምት እንጠቀም። እናምናለን።
, ከዚያም:

እነዚያ።
.

በምርጫ የምንወስነው በየትኛው ዋጋ ነው እኩልነት ይረካል
. ፍቀድ
, ከዚያም
፣ ማለትም እ.ኤ.አ.
. ፍቀድ
, ከዚያም
፣ ማለትም እ.ኤ.አ.
. እንቀበላለን
..

እያንዳንዱን ቃል በ 0.000001 ትክክለኝነት እናሰላለን, ስለዚህ ስንጠቃለል ከ 0.00001 በላይ ስህተት እንዳንይዝ. በመጨረሻም እናገኛለን
.

3. አስላ
በ 0.00001 ትክክለኛነት.

መፍትሄ። አለን።

የሌብኒዝ ፈተናን የመገጣጠም ሁኔታዎችን የሚያረካ ተለዋጭ ተከታታይ ምልክቶች ተገኝተዋል ፣ ስለሆነም በፍፁም እሴት ውስጥ የሚፈቀደው ስህተት ከተከታታዩ የመጀመሪያ ውሎች ያነሰ መሆን አለበት። ያንን ለማየት አስቸጋሪ አይደለም
, ስለዚህ ከተጣሉት ውሎች የመጀመሪያው እኩል ነው
እና
. መጠኑን እናሰላለን እና እናገኛለን
.

4. ማስፋፊያ በመጠቀም
በአንድ ረድፍ, አስላ
ከ 0.0001 ትክክለኛነት ጋር.

መፍትሄ። .

ከዚያ ጀምሮ ተከታታይ ሶስት ውሎችን መውሰድ በቂ ነው።

5. አስላ
ከ 0.0001 ትክክለኛነት ጋር.

በማሰብ በተከታታይ
. አለን።

አራተኛው ቃል ከ 0.0001 ያነሰ ስለሆነ አራተኛውን እና ተከታይ የሆኑትን እንጥላለን. ስለዚህ

6. አስላ
ከ 0.001 ትክክለኛነት ጋር.

መፍትሄ። ምክንያቱም ለቁጥር 130 ቅርብ የሆነ የኢንቲጀር ኪዩብ ነው ፣ ከዚያ 130 ን ቁጥር እንደ የሁለት ቃላት ድምር መወከል ይመከራል።
. ከዚያም

አራተኛው ቃል ያነሰ ነው
, ስለዚህ እሱ እና የሚከተሉት ውሎች ሊወገዱ ይችላሉ. ስለዚህ፣ ማለትም እ.ኤ.አ.
.

7. አስላ
ከ 0.0001 ትክክለኛነት ጋር.

መፍትሄ። ማስፋፊያውን እንጠቀም
በተከታታይ፡-

ወይም ከየት

የተወሰነውን ዋጋ በግምት ከተወሰነ ትክክለኛነት ጋር አስላ , በተገቢው የተመረጠ ተግባር የኃይል ተከታታይ መስፋፋትን በመጠቀም.

8.
.

9.
መልስ፡ 3.017.

10.
መልስ፡ 0.340.

11.
.

12.
,
መልስ፡ 0.84147.

13.
.

14.
መልስ፡ 1.3956.

15.
.

16.
,
መልስ፡ 1.140.

17.
መልስ፡ 0.302.

መልስ፡ 0.464.. የኃይል ተከታታዮች በመገናኘታቸው ክፍተት ውስጥ ባለው ማንኛውም ክፍል ላይ ወጥ በሆነ መልኩ ስለሚሰባሰቡ የተግባር ማስፋፊያዎችን ወደ ሃይል ተከታታዮች በመጠቀም አንድ ሰው በኃይል ተከታታዮች መልክ ያልተወሰነ ውህዶችን ማግኘት እና ተዛማጅ የሆኑ የተወሰኑ ውህዶችን በግምት ያሰላል።

18. አስላ
ከትክክለኛነት ጋር