Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
1. Приближенное вычисление значений функций
Рассмотрим разложение функции в степенной ряд:
Для того, чтобы вычислить приближенное значение функции в заданной точке х , принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r n (x ). Для этого применяют следующие приемы:
Пример 1 . Пользуясь разложением в ряд sinx , вычислить sin20 o с точностью до 0,0001.
Решение
.
Чтобы можно было пользоваться формулой
(2), необходимо выразить значение аргумента
в радианной мере. Получаем
.
Подставляя это значение в формулу,
получаем
Полученный
ряд является знакочередующимся и
удовлетворяет условиям Лейбница. Так
как
,
то этот и все последующие члены ряда
можно отбросить, ограничиваясь первыми
двумя членами. Таким образом,
Пример
2
. Вычислить
с точностью до 0,01.
Решение
.
Воспользуемся разложением
,
где
(см. пример 5 в предыдущей теме):
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
.
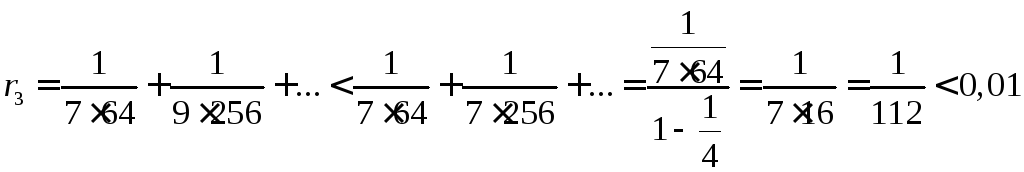Таким образом, мы можем отбросить этот остаток и получаем
.
Пример
3
. Вычислить
с точностью до 0,0001.
Решение . Воспользуемся биномиальным рядом. Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
,
поэтому его и следующие за ним члены
можно отбросить.
2. Приближенное вычисление определенных интегралов
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример
4
: Вычислить
интеграл
с точностью до 0,00001.
Решение
.
Соответствующий неопределенный интеграл
не может быть выражен в элементарных
функциях, т.е. представляет собой
«неберущийся интеграл». Применить
формулу Ньютона-Лейбница здесь нельзя.
Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
.
Пример
5
. Вычислить
интеграл
с точностью до 0,001.
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
Следовательно,
.
Пусть требуется вычислить определенный интеграл $\int\limits_{a}^{b}f(x)dx$ с некоторой наперёд заданной точностью $\varepsilon$. Если непосредственное нахождение первообразной подынтегральной функции $f(x)$ чересчур громоздко, или же интеграл $\int f(x)dx$ вообще не берётся, то в этих случаях можно использовать функциональные ряды. В частности, применяются ряды Маклорена, с помощью которых получают разложение в степенной ряд подынтегральной функции $f(x)$. Именно поэтому в работе нам будет нужен документ с рядами Маклорена .
Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:
- Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
- Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
- Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $\varepsilon$.
Задачи на вычисление интегралов с помощью рядов популярны у составителей типовых расчётов по высшей математике. Поэтому в данной теме мы разберём пять примеров, в каждом из которых требуется вычислить определенный интеграл с точностью $\varepsilon$.
Пример №1
Вычислить $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx$ с точностью до $\varepsilon=10^{-3}$.
Сразу отметим, что интеграл $\int e^{-x^2}dx$ не берётся, т.е. первообразная подынтегральной функции не выражается через конечную комбинацию элементарных функций. Иными словами, стандартными способами (подстановка, интегрирование по частям и т.д.) первообразную функции $e^{-x^2}$ найти не удастся.
Для таких задач есть два варианта оформления, поэтому рассмотрим их отдельно. Условно их можно назвать "развёрнутый" и "сокращённый" варианты.
Развёрнутый вариант оформления
ряд Маклорена :
$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\ldots$$
$$e^{-x^2}=1-x^2+\frac{\left(-x^2\right)^2}{2}+\frac{\left(-x^2\right)^3}{6}+\ldots=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$
Интегрируем полученное разложение на отрезке $\left$:
$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\left(1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots\right)dx=\\ =\left.\left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\ldots\right)\right|_{0}^{1/2}= \frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}-\frac{1}{42\cdot{2^7}}+\ldots$$
Получили сходящийся знакочередующийся ряд. Это значит, что если для вычисления приближенного значения заданного интеграла взять $k$ членов полученного ряда, то погрешность не превысит модуля $(k+1)$-го члена ряда.
Согласно условию, точность $\varepsilon=10^{-3}$. Так как $\frac{1}{42\cdot{2^7}}=\frac{1}{5376}<10^{-3}$, то для достижения требуемой точности достаточно ограничиться первыми тремя членами знакочередующегося ряда:
$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}=\frac{443}{960}.$$
Погрешность полученного равенства не превышает $\frac{1}{5376}$.
Однако суммировать обычные дроби - дело утомительное, поэтому чаще всего расчёты ведут в десятичных дробях:
$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}5}-0{,}0417+0{,}0031\approx{0{,}461}.$$
Разумеется, в этом случае нужно учитывать погрешность округления. Первое слагаемое (т.е. $0{,}5$) было рассчитано точно, поэтому никакой погрешности округления там нет. Второе и третье слагаемые брались с округлением до четвёртого знака после запятой, посему погрешность округления для каждого из них не превысит $0,0001$. Итоговая погрешность округления не превысит $0+0{,}0001+0{,}0001=0{,}0002$.
Следовательно, суммарная погрешность равенства $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$ не превысит $0{,}0002+\frac{1}{5376}<10^{-3}$, т.е. значение интеграла вычислено с требуемой точностью.
Сокращённый вариант оформления
Запишем разложение функции $e^x$ в ряд Маклорена :
$$e^x=\sum\limits_{n=0}^{\infty}\frac{x^n}{n!}$$
Данное разложение верно при всех $x\in{R}$. Подставим $-x^2$ вместо $x$:
$$e^{-x^2}=\sum\limits_{n=0}^{\infty}\frac{\left(-x^2\right)^n}{n!}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}$$
Интегрируем полученный ряд на отрезке $\left$:
$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}dx= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\int\limits_{0}^{\frac{1}{2}}x^{2n}dx=\\ =\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\left.\frac{x^{2n+1}}{2n+1}\right|_{0}^{1/2}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot\left(\frac{1}{2}\right)^{2n+1}}{n!\cdot(2n+1)}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}$$
$$\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}=\frac{1}{2}-\frac{1}{24}+\frac{1}{320}-\frac{1}{5376}+\ldots$$
Все рассуждения, что были сделаны относительно погрешностей в развёрнутом варианте оформления остаются в силе, т.е. $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}461}$.
Чем сокращённый вариант записи лучше развёрнутого?
Во-первых, нам не нужно угадывать, сколько членов ряда взять в изначальном разложении, чтобы вычислить определенный интеграл с заданной точностью. Например, мы записали в самом начале решения:
$$e^{-x^2}=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$
Однако почему мы решили, что нужно взять именно четыре члена ряда? А вдруг нужно взять два члена ряда или пять, или сто? Если бы только шестой член ряда оказался меньше чем $\varepsilon$, - что тогда? А тогда пришлось бы возвращаться в самое начало решения, добавлять ещё пару членов ряда и интегрировать их. А если и этого не хватит, то проделать эту процедуру ещё раз.
Сокращённый вид записи таким недостатком не страдает. Мы получаем числовой ряд, записанный в общем виде, поэтому можем брать столько его членов, сколько потребуется.
Исходя из вышеперечисленных причин, я предпочитаю именно сокращённый способ записи. В дальнейнем все решения в этой теме будут оформлены в сокращённой форме.
Ответ : $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$.
Пример №2
Вычислить определённый интеграл $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx$ с точностью до $\varepsilon=10^{-3}$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.
Начнём с разложения подынтегральной функции $\frac{1-\cos\frac{5x}{3}}{x}$ в ряд Маклорена. Запишем разложение функции $\cos{x}$ в ряд Маклорена :
$$\cos{x}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{(2n)!}$$
Данное разложение верно при всех $x\in{R}$. Подставим вместо $x$ дробь $\frac{5x}{3}$:
$$\cos{\frac{5x}{3}}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{\left(\frac{5x}{3}\right)}^{2n}}{(2n)!}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}.$$
Теперь разложим $1-\cos\frac{5x}{3}$:
$$ 1-\cos\frac{5x}{3}=1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} $$
Забирая из суммы $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$ первый член, получим: $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$. Следовательно:
$$ 1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1-\left(1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}\right)=\\ =-\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} =\sum\limits_{n=1}^{\infty}\frac{-(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}. $$
Последнее, что остаётся - это разделить на $x$:
$$ \frac{1-\cos\frac{5x}{3}}{x}=\frac{1}{x}\cdot\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}. $$
Интегрируем данное разложение на отрезке $\left$:
$$ \int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx=\int\limits_{0}^{\frac{1}{5}}\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}dx= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\int\limits_{0}^{\frac{1}{5}}{x}^{2n-1}dx=\\ =\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\cdot\left.\frac{x^{2n}}{2n}\right|_{0}^{1/5}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}} $$
Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $\varepsilon$):
$$\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}}=\frac{1}{36}-\frac{1}{7776}+\ldots$$
Так как $\frac{1}{7776}<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первого члена полученного числового ряда:
$$\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx\frac{1}{36}\approx{0{,}028}.$$
Ответ : $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx{0{,}028}$.
Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во
Здесь полезно иметь в виду приведенные в предыдущем параграфе разложения в степенные ряды функций e x , shx, chx, sinx, cosx, (1+x) m , ln(1+x), arctgx.
Для вычисления логарифмов эффективна формула
Ряд в правой части равенства сходится тем быстрее, чем больше t .
Для вычисления приближенного значения функции f(х) в ее разложении в степенной ряд сохраняют первые п членов (п- -конечная величина), а остальные члены отбрасывают. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов. Если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. В случае знакопеременного ряда, члены которого удовлетворяют признаку Лейбница, используется оценка < где - первый из отброшенных членов ряда.
403.
0 < x < n+1
∆ Погрешность этого приближенного равенства определяется суммой членов, следующих после х п /п! в разложении е х:
Заменив каждый из сомножителей n+2, n+3, n+4, ... меньшей величиной n+1 , получим неравенство
т.е. 
▲
404 . Вычислить с точностью до 0,00001.
∆ Используя разложение е х в ряд, получаем
Определим число n так, чтобы погрешность приближенного равенства
не превышала 0,00001. Воспользуемся оценкой погрешности, данной в предыдущем, примере. Полагаем х=1/2 ; тогда
т.е. 
Путем подбора определим, при каком значении п будет выполняться неравенство R п < 0,00001. Полагая, например, n= 3 , получаем R 3 < 1/(8·6·7), т. е. R 3 < 1/336. Пусть, далее, n = 5 ; отсюда R 5 < 1/(32·120·11), т. е. R 5 < 1/42240. Пусть, наконец, n= 6 ; отсюда R 6 < 1/(64·720·13) , т. е. R 6 < 1/100000. Итак, принимаем п = 6:
Суммируем слагаемые:
0,020833 (в 6 раз меньше предыдущего слагаемого)
0,002604 (« 8 « « « «)
0,000260 (« 10 « « « «)
0.000022 (« 12 « « « «)
Значит, 
Каждое слагаемое мы вычислили с точностью до 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.
405.
Вычислить сточностью до 0,00001.
∆ Имеем
Воспользуемся приближенным равенством
Мы взяли 5 слагаемых, так как знакопеременный ряд удовлетворяет условиям признака Лейбница, а поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Первый из отброшенных членов равен 1/(5!5 5). Нетрудно видеть, что 1/(5!5 5) < 0,00001.
Произведя вычисления, в результате получаем 
. ▲
406. Пользуясь разложением соsx в ряд, вычислить соs 18° с точностью до 0,0001.
соs 18°= 
;
Достаточно взять три члена ряда, так как (1/6!)-(π/10) 6 < 0,0001. Тогда
. ▲
407. Вычислить с точностью до 0,0001.
∆ Воспользуемся разложением (1+x) m в ряд, полагая x = 0,1, m=1/5 .
Четвертый и следующие за ним члены отбрасываем, так как четвертый член меньше 0,0001. Итак, 
▲
408. Вычислить с точностью до 0,001.
∆ Так как 5 3 является ближайшим к числу 130 кубом целого числа, то целесообразно число 130 представить в виде суммы двух слагаемых: 130 = 5 3 + 5. Тогда
Четвертый член меньше 0,001, поэтому его и следующие за ним члены можно отбросить. Итак, 5 + 0,0667-0,0009, т. е. 5,066. ▲
409.
Вычислить ln1,04 с точностью до 0,0001.
∆ Воспользуемся разложением ln(1+x
) в ряд:
откуда ln1,04≈ 0,0392. ▲
410. В прямоугольном треугольнике катеты равны 1 и 5 см. Определить острый угол треугольника, лежащий против меньшего катета, с точностью до 0,001 радиана.
∆ Так как tgα=1/5, то α=arctg(1,5). Воспользуемся разложением
откуда α ≈ 0,2-0,0027, т. е. α ≈ 0,197. ▲
411. Оценить погрешность приближенного равенства
∆ Задача сводится к оценке суммы остатка ряда
Заменив каждый из множителей 2n+З, 2n + 5, 2n+7, ... меньшим числом 2n+1, получим неравенство
Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:
т.е. 
▲
412. Вычислить ln2 с точностью до 0,0001.
∆ В формуле для определения ln(t + 1) и неравенстве для оценки R п полагаем t= 1:
Путем подбора определим п так, чтобы выполнялось неравенство R n < 0,0001. Если n= 2, то R 2 < 1/(4∙5∙3 3); R 2 < 1/540; если n = 3, то R 3 < 1(4∙7∙3 5); R 3 < 1/6804; если n= 4, то R 4 < 1/(4∙9∙3 7); R 4 < 1/10000.
Итак, n = 4 и для вычисления ln 2 получаем приближенное равенство
в разложении аrctg х.
На примере полученных нами конкретных разложений мы разъясним, как бесконечные ряды могут быть использованы для целей приближенных вычислений. Предпошлем ряд общих замечаний.
Если неизвестное нам число А разложено в ряд:
где - легко вычисляемые (обыкновенно рациональные) числа, и мы положим приближенно:
то поправка на отбрасывание всех остальных членов выразится остатком
При достаточно большом и эта погрешность станет сколь угодно малой, так что воспроизведет А с любой наперед заданной точностью.
Мы заинтересованы в возможности просто производить оценку остатка это позволило бы нам и вовремя остановиться при вычислении последовательных частичных сумм, когда уже будет получено приближение требуемой точности.
Если рассматриваемый ряд оказывается знакопеременным и притом с монотонно убывающими по абсолютной величине членами («цейбницевского типа»), то, как мы видели , остаток имеет знак своего первого члена и по абсолютной величине меньше его. Эта оценка в смысле простоты не оставляет желать лучшего.
Несколько сложнее обстоит дело в случае положительного ряда.
Тогда обыкновенно стараются найти легко суммируемый положительный же ряд, члены которого были бы больше членов интересующего нас остатка, и оценивают остаток суммой этого ряда.
Например, для ряда - можно получить:
[эта оценка совпадает с оценкой сверху, полученной в 373 (11) с помощью интегрирования], а для ряда
[этой оценкой мы фактически и пользовались при вычислении числа в 37].
Обыкновенно ищется десятичное приближение числа А, в то время как члены ряда могут и не быть выражены десятичными дробями. При обращении их в десятичную дробь, округление их служит источником новой погрешности, которую также следует учесть.
Наконец, отметим, что далеко не всякий ряд, имеющий суммой интересующее нас число А, пригоден для фактического вычисления этого числа (даже если его члены просты, и оценка остатка производится легко). Вопрос - в быстроте сходимости, т. е. в быстроте приближения частичной суммы к числу А.
Возьмем для примера ряды [см. 404 (16) и 405 (18)]:
дающие соответственно разложение чисел - и Для того чтобы с их помощью вычислить эти числа, скажем, с точностью до нужно было бы сложить пятьдесят тысяч членов в первом случае и сто тысяч - во втором; это, конечно, осуществимо лишь с помощью быстродействующих вычислительных машин.
Ниже мы без особого труда вычислим упомянутые числа даже с большей точностью, но использовав более подходящие рады.
Лекция 57
РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
Всякая функция,
бесконечно дифференцируемая в интервале
,
т.е.
,
может быть разложена в этом интервале
в сходящийся к ней бесконечный степеннойряд Тейлора
,
если в этом интервале
выполняется условие
,
где
- остаточный член формулы Тейлора,.
При
получаем так называемыйряд Маклорена
:.
Если в некотором
интервале, содержащем точку
,
при любом
выполняется неравенство
,
где
-
положительная постоянная, то
и функция
разложима в ряд Тейлора.
Приведем разложения в ряд Тейлора следующих функций:
1)
2)
7)
8) биномиальный ряд:
Это последнее разложение применимо в следующих случаях:
при
если
при
если
при
если
.
В общем случае разложение функций в степенные ряды основано на использовании рядов Тейлора или Маклорена. На практике степенные ряды многих функций можно найти формально, используя ряды (1-8) или формулу для суммы членов геометрической прогрессии. Иногда при разложении полезно пользоваться почленным дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся к соответствующим функциям.
1.Разложить по
степеням разности
функцию
.
Решение. Для
того, чтобы воспользоваться формулой
Тейлора при
,
найдем:
и т.д.
Следовательно,
2.Разложить
в ряд по степеням
.
Решение.
Воспользуемся равенством
.
Правую часть этого равенства можно
рассматривать как сумму бесконечно
убывающей геометрической прогрессии
с первым членом
и знаменателем
.
Отсюда получаем
Так как
,
то
3. Разложить в
ряд Маклорена функцию
Решение. Разложим данную функцию на сумму простейших рациональных дробей:
Поскольку
то
Так как ряд
сходится при
,
а ряд
сходится
при
,
то ряд
сходится
к данной функции при
.
4.Разложить в
степенной ряд функцию
.
Решение. Найдем
значения функции и ее производных при
Так как
,
то при фиксированном
имеет место неравенство
при любом
.
Следовательно, функция может быть
представлена в виде суммы ряда Тейлора:
.
В данном случае
Это разложение
можно получить и иначе: достаточно в
разложении
заменить
на
.
5. Разложить в
степенной ряд функцию
.
Решение. В разложении
заменяем
на
,
получаем
6. Разложить
в ряд по степеням
.
Решение. В разложении
заменяем
на
,
получаем
7. Разложить в
степенной ряд функцию
.
Решение. Заметим,
что
.Рассмотрим
ряд
Данный ряд сходится
при
,
значит, его можно почленно интегрировать
на любом отрезке
.
Следовательно,
,
т.е получили ряд, сходящийся к данной
функции при
8. Разложить по
степеням
многочлен
9. Разложить по
степеням
функцию
и найти область сходимости полученного
ряда.
Ответ:
10. Разложить по
степеням
функцию
и найти область сходимости этого ряда.
11. Разложить по
степеням
функцию
.
Найти область сходимости этого ряда.
Ответ
Разложить в ряд
Маклорена функцию
.
Указать область сходимости полученного
ряда к этой функции.
12.
.
Ответ:
13.
Ответ:
.
14.
. Ответ:
.
15.
. Ответ:
16.
Ответ:
.
17.
. Ответ:
.
18.
Ответ:
19.
.Ответ:
.
6.16. Применение степенных рядов в приближённых вычислениях
Вычисление
значений функции
. Пусть дан степенной
ряд функции
.
Задача вычисления значения этой функции
заключается в отыскании суммы ряда при
заданном значении аргумента. Ограничиваясь
определенным числом членов ряда, находим
значение функции с точностью, которую
можно установить путем оценивания
остатка числового ряда либо остаточного
члена
формул Тейлора или Маклорена. Если
данный ряд знакопостоянный, то ряд,
составленный из отброшенных членов,
сравнивают с бесконечно убывающей
геометрической прогрессией. В случае
знакочередующегося ряда используется
оценка
,
где
-
первый из отброшенных членов ряда.
Пример 1. Вычислить с точностью до 0,0001 значение ln1,1.
Решение.
Для вычисления приближённых значений функции с заданной точностью удобно пользоваться рядами в том случае, когда соответствующий ряд является знакочередующимся; для знакочередующегося сходящегося ряда легко оценить погрешность приближённого значения суммы – она меньше абсолютного значения первого из отброшенных членов.
Возьмём ряд для функции ln(1+x):
Который сходится к ln(1+x) в интервале (-1,1], и, полагая, x=0,1 , получим ряд для вычисления ln1,1 с любой точностью.
Абсолютное значение четвёртого члена этого ряда меньше 0,0001. Поэтому, согласно свойству знакочередующегося сходящегося ряда, для вычисления приближённого значения ln1,1 с точностью до 0,0001 достаточно взять сумму трёх первых членов ряда
.
Точность: 0,001.
В прикладных задачах важна оценка погрешности приближения.
Определение: Точность вычисления не превышает первого из отброшенных элементов ряда.
1.Оценить погрешность приближенного равенства
Решение.
Погрешность этого приближенного
равенства определяется суммой членов,
следующих после
в разложении
:
,
Заменив каждый
из сомножителей
,…
меньшей величиной
,
получим неравенство
Просуммируем бесконечно убывающую геометрическую прогрессию, получим:
,
т.е.
2.Вычислить
с точностью до 0,00001.
Решение. Используя
разложение
в ряд, получаем
Определим число
так, чтобы погрешность приближенного
равенства
не превышала
0,00001. Воспользуемся оценкой погрешности,
данной в предыдущем примере. Полагаем
,
тогда:
т.е.
.
Путем подбора
определим, при каком значении
будет выполняться неравенство
.
Пусть
,
тогда
,
т.е.
.
Пусть
,
тогда
,
т.е.
.
Принимаем
..
Вычисляем каждое
слагаемое с точностью до 0,000001, для того
чтобы при суммировании не получить
погрешность, превышающую 0,00001. Окончательно
получаем
.
3. Вычислить
с точностью до 0,00001.
Решение. Имеем
Получен
знакочередующийся ряд, удовлетворяющий
условиям сходимости признака Лейбница,
поэтому допускаемая погрешность по
абсолютной величине должна быть меньше
первого из отброшенных членов ряда.
Нетрудно видеть, что
,
поэтому первый из отброшенных членов
равен
и
.
Вычисляем сумму и получаем
.
4. Пользуясь
разложением
в ряд, вычислить
с точностью до 0,0001 .
Решение. .
Достаточно взять три члена ряда, так как Тогда
5. Вычислить
с точностью до 0,0001.
в ряд, полагая
.
Имеем
Четвертый и
следующие за ним члены отбрасываем, так
как четвертый член меньше 0,0001. Итак
6. Вычислить
с точностью до 0,001.
Решение. Так
как
является ближайшим к числу 130 кубом
целого числа, то целесообразно число
130 представить в виде суммы двух слагаемых:
.
Тогда
Четвертый член
меньше
,
поэтому его и следующие за ним члены
можно отбросить. Итак,,
т.е.
.
7. Вычислить
с
точностью до 0,0001.
Решение.
Воспользуемся разложением
в ряд:
или
,
откуда
Вычислить
указанную величину приближенно с
заданной степенью точности
,
воспользовавшись разложением в степенной
ряд соответствующим образом подобранной
функции.
8.
.
Ответ: 3,017.
9.
Ответ: 0,340.
10.
.
Ответ: 0,84147.
11.
.
Ответ: 1,3956.
12.
,
.
Ответ: 1,140.
13.
Ответ: 0,302.
14.
Ответ: 0,464.
15.
Ответ: 1,0986.
16.
,
Ответ: 0,999.
17.
Ответ: 0,3679.
Вычисление интегралов . Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри их интервала сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.
18. Вычислить
с
точностью
Решение.
Воспользуемся разложением
.
Заменив в нем
на
,
получим ряд.
Данный ряд сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,
поскольку уже
третий член полученного знакочередующегося
ряда меньше
19. Найти интеграл
в
виде степенного ряда и указать область
его сходимости.
Решение. Воспользуемся разложением , получим ряд для подынтегральной функции
Он сходится на всей числовой прямой, и, следовательно, его можно почленно интегрировать:
Поскольку при интегрировании степенного ряда его интервал сходимости не изменяется, то полученный ряд сходится также на всей числовой прямой.
Используя
разложение подынтегральной функции в
степенной ряд, вычислить указанный
определенный интеграл с точностью до
.
20.
.
Ответ: 0,070.
21.
.
Ответ: 0,223.
22.
.
Ответ: 0,162.
23.
.
Ответ: 0,480.
24.
.
Ответ: 0,054.
25.
.
Ответ: 0,484.
26.
.
Ответ: 0,487.
27.
.
Ответ: 0,156.
28.
.
Ответ: 0,059.
29.
Ответ: 0,103.
Приближенное решение дифференциальных уравнений .
В случае, когда точно проинтегрировать дифференциальное уравнение с помощью элементарных функций не удается, его решение удобно искать в виде степенного ряда, например ряда Тейлора или Маклорена.
При решении
задачи Коши
,
используется ряд Тейлора
,
где,
а остальные производные
находятся
путем последовательного дифференцирования
уравнения
и подстановки начальных данных в
выражения для этих производных.
Решение задачи
Коши
для
дифференциального уравнения можно
также искать в виде разложения в степенной
ряд
с неопределенными
коэффициентами
.
30. Найти пять
первых членов разложения в степенной
ряд решения
,
если
.
Решение. Из
данного уравнения находим, что
.
Дифференцируем исходное уравнение:
и т.д. Подставляя найденные значения производных в ряд Тейлора, получаем